A.Bērziņa grāmata
BBK2012.P1.1
Vai eksistē 3 viens otram sekojoši skaitļi, kuru reizinājums ir \(19941995199620\)?
BBK2012.P1.2
Vai \(6\) pēc kārtas ņemtu naturālu skaitļu reizinājums var būt \(1111140960\)?
BBK2012.P1.3
Andris saskaitīja sešus viens otram sekojošus naturālus skaitļus un ieguva rezultātu, kurā katrs cipars no \(2\) līdz \(9\) sastopams vienu reizi, bet cipars \(1\) – divas reizes. Pierādīt, ka Andris kļūdījās.
BBK2012.P1.4
Pierādīt, ka skaitlis \(\underbrace{111\ldots{}1}_{\mbox{27 vieninieki}}\) dalās ar \(27\).
BBK2012.P1.5
Pierādīt, ka skaitlis \(\underbrace{111\ldots{}1}_{\mbox{81 vieninieki}}\) dalās ar \(81\).
BBK2012.P1.6
Visi piecciparu skaitļi no \(11111\) līdz \(99999\) patvaļīgā secībā uzrakstīti viens aiz otra. Pierādiet, ka uzrakstītais skaitlis nav divnieka naturāla pakāpe.
BBK2012.P1.7
Aplūkosim visus deviņciparu skaitļus, kuru decimālajā pierakstā katrs cipars no \(1\) līdz \(9\) uzrakstīti tieši vienu reizi. Nosakiet, kāds ir šo skaitļu lielākais kopīgais dalītājs.
BBK2012.P1.8
No skaitļa 1985 atņēma tā ciparu summu, no rezultāta – tā ciparu summu, utt.
(A) Pierādiet, ka noteikti kādreiz iegūsim viencipara skaitli. (B) Kāds tas būs?
BBK2012.P1.9
Reizināšanas pierakstā viens cipars aizstāts ar zvaigznīti.
\[1\ast{}74633 \times 2840332 = 3904414098156.\]
Kas tas par ciparu?
BBK2012.P1.10
Jānis sareizināja visus naturālos skaitļus no \(1\) līdz \(13\) (ieskaitot) un atrada rezultāta otro pakāpi. Iznāca
\[387757880 \ast{} 3632640000,\]
kur viens cipars aizstāts ar zvaigznīti. Atrodiet, kāds cipars aizstāts ar zvaigznīti.
BBK2012.P1.11
No skaitļa \(1230123012301230\) jāizsvītro vairāki cipari tā, lai iegūtais skaitlis dalītos ar \(9\) un būtu maksimāli liels. Kuri cipari jāizsvītro?
BBK2012.P1.12
No nenulles cipariem, katru izmantojot tieši 1 reizi, jāizveido triju trīsciparu skaitļu decimālie pieraksti. Vai var gadīties tā, ka
(A) neviens no tiem nedalās ar \(3\),
(B) tie visi dalās ar \(3\),
(C) divi no tiem dalās ar \(3\), bet trešais – nē?
BBK2012.P1.13
Dots patvaļīgs \(1973\)-ciparu skaitlis, kurš dalās ar \(9\). Šī skaitļa ciparu summu apzīmēsim ar \(a\); skaitļa \(a\) ciparu summu apzīmēsim ar \(b\); skaitļa \(b\) ciparu summu apzīmēsim ar \(c\). Ar ko ir vienāds skaitlis \(c\)?
BBK2012.P1.14
Atrast vislielāko pozitīvo skaitli, ar kuru dalās katrs skaitlis, kas satur visus ciparus (katru tieši vienu reizi).
BBK2012.P1.15
Pierādiet, ka, ja pietiekamā un nepieciešamā dalāmības pazīme ar skaitli \(n\) nav atkarīga no skaitļa ciparu secības, tad \(n\) ir vai nu trīs, vai deviņi.
BBK2012.P1.16
Apzīmēsim skaitļa \(a\) ciparu summu ar \(S(a)\). Pierādiet, ka no vienādības \(S(a) = S(2a)\) seko, ka \(a\) dalās ar \(9\).
BBK2012.P1.17
Skaitli \(A\) pareizinot ar \(3\), tā ciparu summa nemainās. Pierādīt, ka \(A\) dalās ar \(9\).
BBK2012.P1.18
Dots, ka \(n\) – kaut kāds naturāls skaitlis. Skaitlim \(2^n\) atrodam ciparu summu. Iegūtajai summai atkal atrodam ciparu summu, utt. Pieņemsim, ka kādreiz iegūsim desmitciparu skaitli. Pierādīt, ka tam ir vismaz divi vienādi cipari.
BBK2012.P1.19
Vai astoņciparu skaitlis, kura decimālais pieraksts ir simetrisks, var būt pirmskaitlis?
BBK2012.P1.20
Vai četrciparu skaitlis, kura pirmais cipars vienāds ar pēdējo, bet otrais ar trešo var būt pirmskaitlis?
BBK2012.P1.21
Ar vienādiem burtiem apzīmēti vienādi cipari, ar dažādiem burtiem – dažādi. Pierādīt, ka vienādība
\[\text{JĀ}\,\times\,\text{NĒ} \,=\, \text{FFGG}\]
nav pareiza.
BBK2012.P1.22
Pierādiet apgalvojumu: ja skaitlis dalās ar \(99\), tad tā ciparu summa ir ne mazāka kā \(18\).
BBK2012.P1.23
Autobusa biļetei ir sešciparu numurs no \(000000\) līdz \(999999\). Kādu biļešu ir vairāk: tādu, kuru numuru pirmo trīs ciparu summa ir vienāda ar pēdējo trīs ciparu summu, vai tādu, kuru numurs dalās ar \(11\)?
BBK2012.P1.24
Pierādiet, ka skaitlis \(\overline{a_1a_2\cdots{}a_{3m}}\) dalās ar \(7\) (\(11\) vai \(13\)) tad un tikai tad, kad skaitlis
\[\overline{a_1a_2a_3} - \overline{a_4a_5a_6} + \cdots + (-1)^{m-1}\overline{a_{3m-2}a_{3m-1}a_{3m}}\]
dalās ar \(7\) (\(11\) vai \(13\)).BBK2012.P1.25
Kuri no sekojošiem skaitļiem ir pirmskaitļi? Pamatojiet savu atbildi:
(A) \(1395\); (B) \(131313\); (C) \(1993\); (D) \(1991\).
BBK2012.P1.26
Pierādīt, ka sešciparu skaitlis dalās ar \(13\) tādā un tikai tādā gadījumā, ja ar \(13\) dalās tā pirmo trīs ciparu un pēdējo trīs ciparu veidoto skaitļu starpība (mazinātājs varētu sākties ar vienu vai vairākām nullēm).
BBK2012.P1.27
Ar kādu ciparu beidzas reizinājums
\[11 \cdot 12 \cdot 13 \cdot 14 \cdot 15 \cdot 16 \cdot 17 \cdot 18 \cdot 19 \cdot 20 \cdot 21 \cdot 22 \cdot 23 ?\]
BBK2012.P1.28
Četrus veselus pozitīvus skaitļus katru dalīja ar \(5\) ar atlikumu. Iegūto atlikumu summa ir \(3\). Pierādīt, ka šo četru skaitļu reizinājums dalās ar \(5\).
BBK2012.P1.29
Dalot \(1 \cdot 2\) ar \(3\), \(2 \cdot 3\) ar \(4\), \(3 \cdot 4\) ar \(5\), atlikumā iegūst \(2\). Vai vienmēr, dalot divu viens otram sekojošu naturālu skaitļu reizinājumu ar nākošo naturālo skaitli, atlikuma iegūst \(2\)?
BBK2012.P1.30
Pierādīt, ka \(2^{1995} + 2^{1996} + 2^{1997} + 2^{1998}\) dalās ar \(15\).
BBK2012.P1.31
Dots, ka \(a\) un \(b\) ir naturāli skaitļi un \(a+b = 210\). Pierādīt, ka \(ab\) nedalās ar \(210\).
BBK2012.P1.32
Uz skaitļu ass attēloti vairāki veseli skaitļi, kas ņemti pēc kārtas (skat. 1. zīm.):
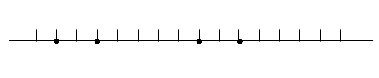
Divi no tiem skaitļiem, kas attēloti ar melniem aplīšiem, dalās ar \(3\), bet divi – ar \(5\) (nav zināms, kuri). Norādiet zīmējumā skaitli, kurš dalās ar \(15\). Pamatojiet savu atbildi.
BBK2012.P1.33
Doti \(6\) stieņi, katrs \(50\) cm garš. Vai tos var sagriezt gabalos tā, lai rastos \(12\) gabali ar garumu \(12\) cm katrs, \(30\) gabali ar garumu \(3\) cm katrs un \(11\) gabali ar garumu \(6\) cm katrs?
BBK2012.P1.34
(A) Vai piecu pēc kārtas ņemtu skaitļu summa var būt \(24\)?
(B) Vai tā var būt \(1984\)?
(C) Vai tā var būt \(1985\)?
BBK2012.P1.35
Naturālus skaitļus no \(1\) līdz \(25\) ieskaitot jāsadala vairākās grupās ( katram skaitlim jānonāk tieši vienā grupā) tā, lai katrā grupā mazākais skaitlis būtu \(8\) reizes mazāks par visu citu šīs grupas skaitļu summu. Vai to var izdarīt?
BBK2012.P1.36
Trīs no aritmētiskās progresijas locekļiem ir \(41\), \(113\), \(193\). Atrast lielāko iespējamo diferences vērtību, ja zināms, ka tā ir vesels skaitlis.
BBK2012.P1.37
Pierādīt, ka \(10a+b\) dalās ar \(7\) tad un tikai tad, ja \(a-2b\) dalās ar \(7\) (\(a\) un \(b\) ir naturāli skaitļi).
BBK2012.P1.38
Dots, ka \(a\) un \(b\) -- naturāli skaitļi un gan \(3a+4b\), gan \(2a+3b\) dalās ar \(7\). Pierādīt, ka gan \(a\), gan \(b\) dalās ar \(7\).
BBK2012.P1.39
Dots, ka \(a\) - naturāls skaitlis, \(p\) - pirmskaitlis, pie tam \(3 a+1\) un \(a-8\) dalās ar \(p\). Aprēķināt \(p\).
BBK2012.P1.40
Naturāli skaitli \(a\) un \(b\) ir tādi, ka \(34a = 43b\). Vai \(a+b\) var būt pirmskaitlis?
BBK2012.P1.41
Dots, ka \(a, b, c\) - dažādi naturāli skaiţ̦li. Kāds lielākais daudzums no skaiţ̦iem \(a+b, \quad a+c, \quad b+c\) var būt pirmskaitļi?
BBK2012.P1.42
Noskaidrojiet
(A) vai visu naturālo skaitļu reizinājums no \(1\) līdz \(76\) ieskaitot dalās ar \(77\);
(B) vai visu naturālo skaitļu reizinājums no \(1\) lîdz \(100\) ieskaitot dalās ar \(101\)?
BBK2012.P1.43
(A) Pierādīt, ka katru \(499\) pēc kārtas n̦emtu naturālu skaitļu reizinājums dalās ar \(1996\).
(B) Vai katru \(498\) pēc kārtas n̦emtu naturālu skaitlu reizinājums dalās ar \(1996\)?
BBK2012.P1.44
(A) atrast kaut vienu \(n\) ar īpašību: jebkuru pēc kārtas n̦emtu \(n\) naturālu skaiţlu summa dalās ar \(1996\),
(B) atrast vismazāko \(n\), kam piemīt (A) punktā minētā īpašība.
BBK2012.P1.45
Kāds lielākais pirmskaitlu daudzums var būt sastopams starp \(12\) pēc kārtas n̦emtiem naturāliem skaitļiem?
BBK2012.P1.46
Zināms, ka dalot skaitlus \(2077\) un \(100\) ar \(a\), iegūti vienādi atlikumi. Kādas var būt skaitļa \(a\) vērtības?
BBK2012.P1.47
Dalot skaitli \(1987\) ar \(a\), atlikumā ieguva skaitli \(9\). Kādas var būt skaitļa \(a\) vērtības?
BBK2012.P1.48
Skaitli \(1991\) dalot ar \(a\), atlikumā iegūst \(9\). Kāds var būt \(a\)?
BBK2012.P1.49
Vai dažādu pirmskaitļu apgriezto lielumu summa var būt vesels skaitlis?
BBK2012.P1.50
Naturāls skaitlis \(A\), dalot ar \(1981\), dod atlikumā \(35\), bet, dalot ar \(1982\), dod atlikumā \(13\). Kādu atlikumu dod \(A\), dalot ar \(14\)?
BBK2012.P1.51
Doti \(12\) pēc kārtas n̦emti naturāli skaitl̦i. Pierādiet, ka vismaz viens no tiem ir mazāks par savu dalītāju summu. (Tiek ņemti skaița naturālie dalītāji, kas mazāki par pašu skaitli).
BBK2012.P1.52
Vai iespējams norādīt tādu galīgu skaitu ģeometrisko progresiju, kuru locekļi ir naturāli skaitļi, ka jebkurš naturāls skaitlis piederētu vismaz vienai progresijai?
BBK2012.P1.53
(A) Atrast mazāko naturālo skaitli, kuru
- dalot ar \(2\), iegūst atlikumā \(1\);
- dalot ar \(3\), iegūst atlikumā \(2\);
- dalot ar \(4\), iegūst atlikumā \(3\);
- dalot ar \(5\), iegūst atlikumā \(4\);
- dalot ar \(6\), iegūst atlikumā \(5\).
(B) Atrast mazāko naturālo skaitli, kuru dalot ar \(n, n+1, \ldots, n+m\), iegūst atlikumā atbilstoši \(r, r+1, \ldots, r+m\).
BBK2012.P1.54
Noteikt, kāds varēja būt mazākais kokosriekstu skaits, ko savāca pieci jūrnieki uz neapdzīvotas salas, ja viṇi dalīja kokosriekstus šādi: pirmais no viņiem, kamēr pārējie gulēja, iedeva vienu riekstu pērtiķim un paņēma sev \(\frac{1}{5}\) no atlikušajiem riekstiem; tālāk tieši tāpat pēc kārtas rīkojās visi pārējie jūrnieki. Pēc tam visi kopā vēl vienu reizi dalīja riekstus: Vienu iedeva pērtiķim, bet pārējos sadalīja savā starpā piecās vienādās daļās.
BBK2012.P1.55
Dots, ka \(a, b, c\) - naturāli skaitļi. Cik daudzi no skaitļiem \(a+b\), \(a+c\), \(b+c\) var vienlaikus dalîties ar \(3\)?
BBK2012.P1.56
Atrast kaut vienu veselu skaitli \(n\), kas apmierina divas šādas īpašības:
a. \(n\) nedalās ne ar vienu no skaițiem \(2,3,4,5,6,7,8,9,10\), b. \(n-1\) dalās ar katru no skaitļiem \(2,3,4,5,6,7,8,9,10\).
BBK2012.P1.57
Kāds ir lielākais daudzums pēc kārtas n̦emtu naturālu trīsciparu skaitlu, no kuriem nevienu nevar izsacìt kā divu (dažādu vai vienādu) divciparu skaitļu reizinājumu?
BBK2012.P1.58
Vai iespējama vienādība \(a,bc=\overline{ab}: c\) ?
Piezīme: \(a,bc\) ir decimāldala ar ciparu \(a\) pirms komata un cipariem \(b\) un \(c\) aiz komata; \(\overline{ab}\) ir divciparu skaitlis.
BBK2012.P1.59
Ar \(\overline{xyz}\) apzīmēsim trīsciparu skaitli ar cipariem \(x,y,z\). Pierādīt, ka, ja \(\overline{abc}\) dalās ar \(37\), tad arī \(\overline{bca}+\overline{cab}\) dalās ar \(37\).
BBK2012.P1.60
Atrast visus divciparu skaitlus, kuru summa ar skaitli, kas pierakstitts ar tiem pašiem cipariem otrādā kārtībā, ir naturāla skaiţ̦a kvadrāts.
BBK2012.P1.61
Atrast visus naturālos divciparu skaitlus, kam piemīt īpašība: šī skaiț̣a un skaiţ̦a, kuru iegūst mainot tā ciparus vietām, starpība ir kāda naturāla skaiţ̦a kvadrāts.
BBK2012.P1.62
Atrisināt pirmskaiţ̦os vienādojumu
\[x^{3}-y^{3}=z.\]
BBK2012.P1.63
Doti četri naturāli skaiţ̧i \(a, b, c, d\), kuri ir savstarpēji pirmskaitļi ar skaitli \(m = ad - bc\). Pierādiet, ka visām veselām \(x\) un \(y\) vērtībām, kurām \(ax + by\) dalās ar \(m\), skaitlis \(cx + dy\) arī dalās ar \(m\).
BBK2012.P1.64
Doti tādi veseli skaiţ̦i \(u\) un \(v\), ka \(u^{2}+u v+v^{2}\) dalās ar 9. Pierādiet, ka abi skaitlii \(u\) un \(v\) dalās ar \(3\).
BBK2012.P1.65
Pierādiet, ka naturāls skaitlis \(n\) ir pirmskaitlis tad un tikai tad, kad eksistē viens vienīgs skaitļu pāris \((x, y)\), kuram izpildās vienādība \(\frac{1}{x}-\frac{1}{y}=\frac{1}{n}\).
BBK2012.P1.66
Atņemot no divciparu skaița \(\overline{ab}\) divciparu skaitli \(\overline{ba}\), ieguva naturāla skaiţ̦a kubu. Atrast visus tādus skaiţlus, kuriem izpildās šāda īpašība.
BBK2012.P1.67
Pirmo \(n\) naturālo skaitlu summa ir trīsciparu skaitlis, kuram visi cipari ir vienādi. Atrast skaitli \(n\).
BBK2012.P1.68
Zināms, ka divu dotu racionālu skaitlu summa un reizinājums ir veseli skaitļi.
(A) Pierādīt, ka dotie skaitļi paši ir veseli.
(B) Vai apgalvojums paliek spēkā, ja nav zināms, ka dotie skaitļi ir racionāli?
BBK2012.P1.69
Naturālu skaitli sauc par interesantu, ja tā ciparu summa dalās ar \(5\).
(A) Atrast kaut vienu tādu interesantu \(x\), ka ari \(x+9\) ir interesants,
(B) Cik pavisam ir tādu interesantu \(x\), kādi minēti (A) punktā?
(C) Pierādīt: starp jebkuriem 9 pēc kārtas n̦emtiem naturāliem skaitliem ir vismaz viens interesants.
BBK2012.P1.70
Atrodiet divciparu skaitli, kurš ir vienāds ar otrā cipara kvadrāta un pirmā cipara summu.
BBK2012.P1.71
Atrodiet trīsciparu skaitli, kuru kāpinot jebkurā naturālā pakāpē, iegūstam skaitli, kura pēdējie trīs cipari veido sākotnējo skaitli.
BBK2012.P1.73
Dots naturāls skaitlis \(m\). Noteikt cik daudz ir tādu veselu nenegatīvu skaitlu \(k\), kuriem \(m+k^{2}\) ir pilns kvadrāts.
BBK2012.P1.74
Pierādiet, ka pirmos \(n\) naturālos skaitlus nevar sadalīt divās grupās tā, lai visu vienas grupas skaitlu reizinājums būtu vienāds ar visu otrās grupas skaitḷu reizinājumu.
BBK2012.P1.75
Atrodiet visus tādus naturālus skaitlus \(m\), kuriem izpildās vienādība
\[1! \cdot 3! \cdot 5! \cdot \cdots \cdot (2m-1)! = \left(\frac{m(m+1)}{2}\right)!\]
BBK2012.P1.76
Skolotājs uzrakstīja uz tāfeles naturālu skaitli. Pirmais skolnieks pateica, ka šis skaitlis dalās ar \(2\), otrais -- ka šis skaitlis dalās ar \(3\), utt., trīsdesmitais -- ka šis skaitlis dalās ar \(31\). Izrādījās, ka \(28\) skolnieki ir pateikuši taisnību, bet divi, ka atbildēja viens pēc otra, ir kļūdījušies. Kuri no skolniekiem kḷūdījās?
BBK2012.P1.77
Atrodiet visus reālu skaitļu trijniekus \((a, b, c)\), kuriem visi skaitļi \(\frac{a}{b}+\frac{b}{c}\), \(\frac{b}{c}+\frac{c}{a}, \frac{c}{a}+\frac{a}{b}\) ir veseli.
BBK2012.P1.78
Pien̦msim, ka \(p\) un \(q\) ir divi viens otram sekojoši nepāra pirmskaitļi. Pierādīt, ka \(p+q\) ir vismaz trīs naturālu skaitļu reizinājums, katrs no kuriem ir lielāks par \(1\).
BBK2012.P1.79
Vai \((n-1)!\) dalās ar \(n\), ja
(A) \(n=16\),
(B) \(n=41\),
(C) \(n=1991\),
(D) \(n=1993\)?
BBK2012.P1.80
Pierādīt, ka var atrast \(1000\) pēc kārtas ņemtus naturālus skaitļus starp kuriem nav neviena pirmskaitļa.
BBK2012.P1.81
Pierādiet, ka mazākais naturālais skaitlis \(N>1\), kurš ir savstarpējais pirmskaitlis ar skaițiem \(1,2, \ldots, n\), ir pirmskaitlis.
BBK2012.P1.82
Pierādiet, ka eksistē bezgalīgi daudz tādu pirmskaitlu \(q\), kuriem eksistē tāds naturāls skaitlis \(n<q\), ka skaitlis \((n-1)!+1\) dalās ar \(q\).
BBK2012.P1.83
Kādiem naturāliem \(n\) skaitlis \((n-1)!\) nedalās ar \(n\)?
BBK2012.P1.84
Dots nepāra skaitlis \(n>1\). Pierādiet, ka \(n\) un \(n+2\) ir pirmskaitļi tad un tikai tad, kad \((n-1)!\) nedalās ne ar \(n\), ne ar \(n+2\).
BBK2012.P1.85
Ar \(n?\) apzīmēsim visu pirmskaitḷu reizinājumu, kuri nepārsniedz \(n\). Pierādiet, ka visiem \(n \geq 4\) izpildās nevienādība \((n-1)? > n\).
BBK2012.P1.86
Ar \(p_{n}\) apzīmēsim \(n\)-to pēc kārtas pirmskaitli. Pierādiet, ka visiem naturāliem \(n\) izpildās nevienādība \(p_{n}<2^{2^{n}}\).
BBK2012.P1.87
Pierādiet, ka eksistē bezgalīgi daudz tādu pirmskaitļu \(p\), ar kuriem vienādojumam \(x^{2}+x+1 = py\) eksistē atrisinājums veselos skaitļos.
BBK2012.P1.88
Ar \(q_{n}\) apzīmēsim mazāko pirmskaitli, kurš nav \(n\) dalītājs. Pierādiet, ka \(\lim _{n \rightarrow \infty} \frac{q_{n}}{n}=0\).
BBK2012.P1.89
Pierādīt, bezgalīgi daudziem pirmskaitļiem \(p\) var atrast tādus naturālus skaitļus \(x\) un \(y\), ka \(2x^2 + 2x + 1 = py\).
BBK2012.P1.90
Dots, ka \(a\) un \(b\) ir divi naturāli skaitļi. Vai var būt, ka to lielākais kopējais dalītājs ir \(32\), bet to mazākais kopīgais dalāmais ir \(1200\)?
BBK2012.P1.91
Pierādīt, ka skaiţu \(19951995\) un \(19952003\) lielākais kopīgais dalītājs ir \(1\).
BBK2012.P1.92
Dots naturāls skaitlis \(n\). Pierādīt, ka abi skaiț̣i \(2n+5\) un \(3n+8\) vienlaicīgi nedalās ne ar kādu naturālu skaitli, kas lielāks par \(1\).
BBK2012.P1.93
Dots, ka \(n\) - naturāls skaitlis. Pierādīt, ka \(3n+2\) un \(7n+5\) ir savstarpēji pirmskaitļi.
BBK2012.P1.94
Aritmētiskā progresija, kuras locekļi ir veseli skaitļi satur skaitļus \(13\), \(37\) un \(79\). Kāda var būt lielākā šīs progresijas diferences vērtība?
BBK2012.P1.95
Atrodiet kaut vienu tādu naturālu skaitli \(n\), ka \(n\) dalās ar \(6,(n+1)\) dalās ar \(5\), \((n+2)\) dalās ar \(4\), \((n+3)\) dalās ar \(3\), \((n+4)\) dalās ar \(2\).
BBK2012.P1.96
Dots, ka \(n\) dalās ar \(6\), \(n\) - naturāls skaitlis. Pierādīt, ka \(n\) var sadalīt triju dažādu veselu pozitīvu saskaitāmo summā tā, lai katriem diviem no tiem lielākais kopīgais dalītājs būtu \(1\).
BBK2012.P1.97
Pierādīt, ka katru naturālu skaitli, kas lielāks par \(17\), var izsacīt kā triju tādu naturālu skaitļu summu, no kuriem katriem diviem lielākais kopīgais dalītājs ir \(1\).
BBK2012.P1.98
Doti naturāli skaitļi \(x\) un \(y\); \(u\) ir to lielākais kopigais dalītājs, \(v\) ir to mazākais kopīgais dalāmais. Atrisināt vienādojumu sistēmu.
\[\left\{\begin{array}{l} x \cdot y \cdot u \cdot v = 3600 \\ u + v = 32 \\ \end{array}\right.\]
BBK2012.P1.99
Virknē uzrakstīti cipari no \(1\) līdz \(9\):
\[1\;\;2\;\;3\;\;4\;\;5\;\;6\;\;7\;\;8\;\;9\]
Kādu lielāko daudzumu semikolu var ievietot starp blakus esošiem cipariem, lai tie sadalītu ciparu virkni tādu naturālo skaitļu pierakstos, no kuriem katriem diviem lielākais kopīgais dalītājs ir \(1\)? (Piemēram, pieraksts \(123;45678;9\) neder, jo \(123\) un \(9\) abi dalās ar \(3\).)BBK2012.P1.100
Sešciparu skaitļa \(N\) pirmais cipars ir \(7\), piektais - \(2\), bet pēdējais - nepāra skaitlis. Zināms, ka dalot \(N\) ar skaiţ̧iem \(3\), \(4\), \(7\), \(9\), \(11\) un \(13\), rezultātā iegūstam vienādus atlikumus. Atrodiet skaitli \(N\).
BBK2012.P1.101
Doti naturāli skaitļi \(a_{1}<a_{2}<\cdots<a_{n}\). Pierādiet, ka \(\left[ a_{1}, a_{2}, \ldots, a_{n} \right] \geq n a_{1}\).
BBK2012.P1.102
Doti naturāli skaitļi \(a\) un \(b\). Pierādiet, ka no skaitļiem \(a, 2a, 3a, \ldots, ba\) tieši \((a,b)\) dalās ar \(b\).
BBK2012.P1.103
Doti veseli skaitļi \(a\) un \(b\). Pierādiet, ka skaitļu \(a+b\) un \(a^{2}+b^{2}\) LKD ir vienāds ar \(1\) vai \(2\).
BBK2012.P1.104
Skaitļu virkne \((a_i)\) tiek definēta šādi:
\[a_1=19,\;a_2=90,\;a_{n+2}=a_n+a_{n+1},\;\mbox{ja}\;n=1,2,3,\ldots.\]
Atrast skaitļu \(a_{1989}\) un \(a_{1990}\) lielāko kopīgo dalītāju.BBK2012.P1.105
Kādu lielāko vērtību var pieņemt skaitļu \(a_{1}, a_{2}, \ldots, a_{10}\) LKD, ja to summa ir \(1001\)?
BBK2012.P1.106
Skaitļi \(a_{1}, a_{2}, a_{3}, \ldots, a_{10}\) ir veseli pozitīvi skaitļi un
\[a_{1}+a_{2}+a_{3}+\cdots+a_{10}=1001\]
Kādas vērtības var būt skaitļu \(a_{1}, a_{2}, a_{3}, \ldots, a_{10}\) lielākajam kopīgajam dalītājam?BBK2012.P1.107
Skaitlis \(2401\) ir izteikts kā \(25\) naturālu skaitļu summa. Kāda ir mazākā iespējamā šo skaitļu MKD vērtība?
BBK2012.P1.108
Kādu lielāko daudzumu naturālu skaitļu, kas nepārsniedz \(360\), var izvēlēties tā, lai neviens no tiem nebūtu pirmskaitlis, bet katru divu izraudzīto skaitļu lielākais kopīgais dalītājs būtu \(1\)?
BBK2012.P1.109
Pierādīt, ka no katriem
(A) trim,
(B) pieciem,
(C) septiņiem
pēc kārtas n̦emtiem naturāliem skaiţ̦iem var izvēlēties vienu tā,
ka tas ir savstarpējs pirmskaitlis ar katru no pārējiem.
BBK2012.P1.110
Doti naturāli skaiţ̧i \(a\) un \(b\). Zināms, ka \(\frac{a+1}{b}+\frac{b+1}{a}\) ir vesels skaitlis. Pierādīt, ka \((a, b) \leq \sqrt{a+b}\).
BBK2012.P1.111
Doti naturāli skaiţ̦i \(a, b, a^{\prime}, b^{\prime}\). Apzīmēsim \((a, b)\) ar \(d\) un \(a^{\prime}, b^{\prime}\) ar \(d^{\prime}\). Pierādīt, ka \(\left(a a^{\prime}, a b^{\prime}, b a^{\prime}, b b^{\prime}\right)=d d^{\prime}\).
BBK2012.P1.112
Vai skaitlis \(x\) noteikti ir racionāls, ja zināms, ka racionāli ir sekojoši skaitļi
(A) \(x^{55}\) un \(x^{89}\),
(B) \(x^{91}\) un \(x^{42}\)?
BBK2012.P1.113
Doti naturāli skaiţ̦i \(a, b, c\), kuriem \((a, b, c)=1\), un izpildās vienādība
\[\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\]
Pierādiet, ka \(a+b\) ir naturāla skaiţ̦a kvadrāts.BBK2012.P1.114
Naturāliem skaiţ̧iem \(x, y, z\) izpildās vienādība \(\frac{1}{x}-\frac{1}{y}=\frac{1}{z}\). Skaitļu \(x, y, z\) lielākais kopīgais dalītājs ir \(h\). Pierādīt, ka skaitļi \(h x y z\) un \(h(y-z)\) ir kvadrāti.
BBK2012.P1.115
Atrodiet visus tādus dažādu naturālu skaitļu trijniekus, kuriem skaitļi \(ab\), \(ac\) un \(bc\) veido aritmētisko progresiju.
BBK2012.P1.116
Dots naturāls skaitlis \(n\). Aplūkosim tādu naturālu skaiţ̦u pārus \((u, v)\), kuriem \([u, v]=n\). Pierādiet, ka šādu pāru skaits ir vienāds ar skaiț̣a \(n^{2}\) pozitīvo dalītāju skaitu.
BBK2012.P1.117
Aplūkojam visus naturālos skaitļus no \(1\) līdz
\(2\,000\,000\) ieskaitot. Izvēlēsimies
no tiem kaut kādus \(1\,000\,001\) skaitļus.
(A) Pierādīt, ka starp izvēlētajiem skaitļiem
noteikti atradīsies divi tādi, kas ir savstarpēji
pirmskaitļi.
(B) Vai to noteikti var apgalvot, ja tiek izvēlēti
\(1\,000\,000\) skaitļi?
BBK2012.P1.118
Uz tāfeles uzrakstìti 1999 naturāli skaiţ̦i (starp tiem var būt arī vienādi). Ar vienu gājienu aţ̦auts nodzēst divus skaitlus un to vietā uzrakstīt nodzēsto skaitlu lielāko kopīgo dalītāju un mazāko kopīgo dalāmo.
Pierādīt, ka izdarot šādus gājienus pietiekami ilgi, uz tāfeles uzrakstītie skaitļi kādreiz pārstās mainīties.
BBK2012.P1.119
Doti naturāli skaitļi \(a\), \(b\) un \(m\); \(\mbox{LKD}(a,b)=1\). Pierādiet, ka aritmētiskajā progresijā \(ak+b\), (\(k=0,1,2,\ldots\)) ir bezgalīgi daudz locekļu, kas ir savstarpēji pirmskaitļi ar skaitli \(m\).
BBK2012.P1.120
Doti \(12\) dažādi naturāli skaiţ̦li. Katriem \(5\) no tiem mazākais kopīgais
dalāmais ir viens un tas pats skaitlis \(M\). Ir zināms, ka no dotajiem
\(12\) skaitliem var izvēlēties \(x\) skaiţ̧us tā, ka katri divi no izvēlētajiem
skaiţ̦liem ir savstarpēji pirmskaitļi.
(A) Pierādīt, ka \(x \leq 4\).
(B) Pierādīt, ka var gadīties, ka \(x=4\).
BBK2012.P1.121
Dota virkne \(x_1=19,\;x_2=95,\;x_{n+2}=\mbox{LKD}(x_{n+1},x_n)+x_n\), ja \(n \geq 1\). Atrast skaitļu \(x_{1995}\) un \(x_{1996}\) lielāko kopīgo dalītāju.
BBK2012.P1.122
Cik daudz ir tādu naturālu skaitļu \(n \leq 1983\), kuriem \(3n+5\) dalās ar \(7\)?
BBK2012.P1.123
Cik daudz ir tādu naturālu skaitļu \(n \leq 1000\), kuri nedalās ne ar \(5\), ne ar \(7\)?
BBK2012.P1.124
Atrast
(A) visu to naturālo skaitļu summu, kas nepārsniedz \(1000\) un dalās ar \(5\);
(B) visu to naturālo skaitļu summu, kas nepārsniedz \(1000\) un dalās
vai nu ar \(3\), vai ar \(5\).
BBK2012.P1.125
Cik daudz tādu piecciparu skaitļu, kuru pēdējais cipars ir \(6\), un kuri dalās ar \(3\)?
BBK2012.P1.126
No naturāliem skaitļiem, kas nepārsniedz \(1993\), izvēlieties \(1328\) skaitļus tā, lai starp jebkuriem trim izvēlētajiem būtu vismaz divi, kuru lielākais kopīgais dalītājs pārsniedz vieninieku. Pietiek uzrādīt vienu šādu \(1328\) skaitļu komplektu.
BBK2012.P1.127
Pierādīt, ka jebkuriem naturāliem skaitļiem \(n\) un \(k\) izpildās vienādība
\[\left\lfloor \frac{n}{k} \right\rfloor + \left\lfloor \frac{n+1}{k} \right\rfloor + \ldots + \left\lfloor \frac{n+k-1}{k} \right\rfloor = n.\]
BBK2012.P1.128
Ar \(\lfloor x \rfloor\) apzīmē lielāko veselo skaitli, kas nepārsniedz \(x\). Pierādīt: ja \(p\) un \(q\) – naturāli skaitļi, kuru lielākais kopīgais dalītājs ir \(1\), tad
\[\left\lfloor \frac{p}{q} \right\rfloor + \left\lfloor \frac{2p}{q} \right\rfloor + \left\lfloor \frac{3p}{q} \right\rfloor + \ldots + \left\lfloor \frac{(q-1)p}{q} \right\rfloor =\]
\[=\left\lfloor \frac{q}{p} \right\rfloor + \left\lfloor \frac{2q}{p} \right\rfloor + \left\lfloor \frac{3q}{p} \right\rfloor + \ldots + \left\lfloor \frac{(p-1)q}{p} \right\rfloor.\]
BBK2012.P1.129
Dots naturāls skaitlis \(n\). Aprēķināt summu
\[\left\lfloor \frac{n+1}{2} \right\rfloor + \left\lfloor \frac{n+2}{2^2} \right\rfloor + \ldots + \left\lfloor \frac{n+2^k}{2^{k+1}} \right\rfloor + \ldots.\]
BBK2012.P1.130
Pierādīt, ka vienādība
\[\sum_{k=1}^n \left\lfloor \frac{n}{k} \right\rfloor = 2 + \sum_{k=1}^{n-1} \left\lfloor \frac{n-1}{k} \right\rfloor,\; n \in \mathbb{N}, n\geq 2\]
izpildās tad un tikai tad, kad \(n\) ir pirmskaitlis.BBK2012.P1.131
Atrodiet visus tādus naturālus skaitļus \(k\), kuriem virkne \(k+1,k+2,\ldots,k+100\) satur maksimālo iespējamo pirmskaitļu skaitu.
BBK2012.P1.132
Ar \(d(i)\) apzīmēsim skaitļa \(i\) naturālo dalītāju skaitu. Pierādiet, ka jebkuram naturālam skaitlim \(n\) izpildās vienādība
\[d(1)+d(2)+\ldots+d(n)= \left\lfloor \frac{n}{1} \right\rfloor + \left\lfloor \frac{n}{2} \right\rfloor + \ldots + \left\lfloor \frac{n}{n} \right\rfloor.\]