Tēma

2.2.0.0.0. Grafu uzdevumi

Uzdevumi, kuros ir dots skaits objektu, starp katriem diviem no tiem var būt vai nebūt attiecība. Uzdevumi par draudzībām, pazīšanos, ceļiem starp pilsētām, saziņu ar vēstulēm vai pa telefonu.

LV.AMO.2003.5.4

Vai kvadrātā, kas sastāv no \(4 \times 4\) rūtiņām, var katrā rūtiņā ierakstīt naturālu skaitli no \(1\) līdz \(16\) (tiem visiem jābūt dažādiem) tā, lai nekādi divi skaitļi, kas ierakstīti rūtiņās ar kopīgu malu, abi vienlaicīgi nedalītos ne ar vienu citu naturālu skaitli kā \(1\)?

LV.AMO.2011.5.4

Vai naturālos skaitļus no \(1\) līdz \(12\), katru izmantojot tieši vienu reizi, var uzrakstīt pa apli tādā secībā, ka jebkuru divu blakus esošu skaitļu starpība ir

(A) \(2\) vai \(3\);
(B) \(3\) vai \(4\)?

LV.AMO.2023.5.4

Dots kvadrāts ar izmēriem \(n \times n\) rūtiņas. Vienā gājienā kauliņu var pārlikt tieši \(2\) rūtiņas uz priekšu pa jebkuru no diagonālēm, kas iziet no tā lauciņa, kurā atrodas kauliņš (skat. 4. att., kur kauliņš apzīmēts ar "o" un ar "x" atzīmētas tās rūtiņas, uz kurām to drīkst pārvietot). Vai, veicot vairākus gājienus, kauliņu no kreisās apakšējās rūtiņas var pārvietot uz kreiso augšējo rūtiņu, ja kvadrāta izmēri ir: (A) \(9 \times 9\); (B) \(10 \times 10\); (C) \(11 \times 11\)?
4.zīm.

LV.AMO.2003.6.4

Šaha turnīrā katrs spēlētājs ar katru citu spēlēja vienu reizi. Par uzvaru iegūst \(1\) punktu, par neizšķirtu \(\frac{1}{2}\) punkta, par zaudējumu - \(0\) punktus. Jānis, Pēteris, Andris un Juris ieguva attiecīgi \(4 \frac{1}{2}\), \(3 \frac{1}{2}\), \(3\) un \(1 \frac{1}{2}\) punktus; neviens no citiem spēlētājiem neieguva vairāk punktu nekā Juris. Cik bija citu spēlētāju un cik punktus viņi ieguva?

LV.AMO.2007.7.1

Kādu lielāko daudzumu dažādu ciparu var izrakstīt pa apli tā, lai katri divi blakus uzrakstīti cipari, lasot tos vienalga kādā virzienā, veidotu pirmskaitļa pierakstu?

LV.AMO.2023.7.1

Vai rindā kaut kādā secībā var uzrakstīt naturālus skaitļus (A) no \(1\) līdz \(23\); (B) no \(1\) līdz \(2023\) tā, lai blakus skaitļiem nebūtu vienādu ciparu?

LV.AMO.2024.7.3

Skaitḷu virknes pirmais loceklis ir \(12\). Katru nākamo iegūst iepriekšējo vai nu reizinot ar \(2\) vai \(3\), vai arī izdalot ar \(2\) vai \(3\) (ja tas dalās bez atlikuma). Vai šīs skaitļu virknes 61.loceklis var būt skaitlis \(54\)?

LV.NOL.2015.7.3

Tabulā, kuras izmēri ir \(3 \times 3\) rūtiņas, katrā rūtiņā ierakstīts viens naturāls skaitlis, kas nepārsniedz \(10\), visi ierakstītie skaitļi ir dažādi. Katrām divām rūtiņām ar kopīgu malu aprēķina tajos ierakstīto skaitļu summu. Vai iespējams, ka visas iegūtās summas ir pirmskaitļi?

LV.AMO.2014.8.3

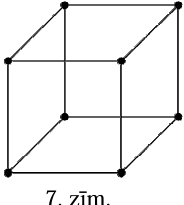
Astoņi punkti savienoti ar šķautnēm kā kuba karkass (skat. 7.zīm.). Pierādīt, ka, izvēloties jebkurus \(5\) punktus, tie būs savienoti ar vismaz \(3\) šķautnēm!

LV.AMO.2019.8.4

Mežā dzīvo \(m\) rūķīši. Daži no tiem savā starpā draudzējas (ja \(A\) draudzējas ar \(B\), tad \(B\) draudzējas ar \(A\)), pie tam katra rūķīša draugu skaits ir kāda naturāla skaitļa kubs. Kādām \(m\) vērtībām tas ir iespējams?

LV.AMO.2022B.8.4

Is it possible to arrange the numbers
(A) \(0;\;1;\;2;\;3;\;4;\;5;\;6;\;7;\;8;\;9\)
(B) \(0;\;1;\;2;\;3;\;4;\;5;\;6;\;7;\;8;\;9;\;10;\;11;\;12;\;13\)
around a circle so that any two adjacent numbers differ by \(3\), \(4\), or \(5\)?

LV.AMO.2022B.8.4

Vai pa apli var uzrakstīt skaitļus
(A) \(0;\;1;\;2;\;3;\;4;\;5;\;6;\;7;\;8;\;9\); (B) \(0;\;1;\;2;\;3;\;4;\;5;\;6;\;7;\;8;\;9;\;10;\;11;\;12;\;13\); tā, lai katri divi blakus esoši skaitļi atšķirtos par \(3\); \(4\) vai \(5\)?

LV.AMO.2024.8.3

Trīs burvji rituālā spēj pārveidot skaitļus, bet katrs no burvjiem prot tikai vienu burvestību:

pirmais burvis spēj atņemt no jebkura skaitḷa \(1\);
otrais burvis spēj izdalīt jebkuru skaitli ar \(2\);
trešais burvis spēj reizināt jebkuru skaitli ar \(3\).

Lai pārveidotu skaitli, burvji var pielietot savas burvestības jebkurā secībā, pat izlaižot citus burvjus. Bet katrs burvis savu burvestību katrā rituālā drīkst izmantot tikai \(5\) reizes, un starprezultātam jābūt veselam skaitlim, kas nepārsniedz \(9\). Vai burvji rituālā no skaitliem \(3,8,9,2,4\) var iegūt (A) \(3,3,3,3,3\); (B) \(5,5,5,5,5\)?

LV.AMO.2017.9.4

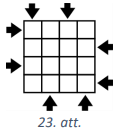
(A) Pierādi, ka dotajā \(4 \times 4\) rūtiņu laukumā (skat. 23.att.) nevar ierakstīt \(16\) dažādus naturālus skaitļus tā, lai katrā rūtiņā būtu ierakstīts viens skaitlis un katrā rindā un katrā kolonnā skaitļi pieaugtu bultiņas norādītajā virzienā.

(B) Kāds mazākais bultiņu skaits jāapvērš pretējā virzienā, lai skaitļus varētu izvietot saskaņā ar uzdevuma nosacījumiem?

LV.AMO.2018.9.4

Atrast lielāko naturālo skaitli, kas dalās ar \(7\), kura ciparu summa ir \(100\) un kuram neviens cipars nav \(0\).

LV.AMO.2022B.9.4

Is it possible to arrange the numbers
(A) \(1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13\);
(B) \(1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14\)
on a circle so that any two adjacent numbers differ by \(3\); \(4\) or \(5\)?

LV.AMO.2022B.9.4

Vai pa apli var uzrakstīt skaitļus
(A) 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13;
(B) 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14;
tā, lai katri divi blakus esoši skaitļi atšķirtos par \(3\); \(4\) vai \(5\)?

LV.AMO.2022B.9.5

The floor plan of the art museum shall is a rectangle of size (A) \(8 \times 9\); (B) \(9 \times 11\) squares, where one square corresponds to a single museum room. The director of the museum wants to create a visitor route that satisfies the following requirements:

the route starts in one of the squares (rooms) at the edge of the rectangle;
a visitor on his route can move from one square (room) to another square (room), if they share a common side.
the visitor enters each square (room) exactly once during the route;
the route ends in a square (room) at the edge of the rectangle and is located next to the square (room) that started the route.

Can the director of the museum create such route?

LV.AMO.2022B.9.5

Mākslas muzeja plānojums ir taisnstūris ar izmēriem (A) \(8 \times 9\); (B) \(9 \times 11\) rūtiņas, kur viena rūtiņa atbilst vienai muzeja telpai. Muzeja vadītājs vēlas izveidot apmeklētāju maršrutu, kuram izpildās šādas īpašības:

maršruts sākas kādā no rūtiņām (telpām), kas atrodas pie taisnstūra malas;
apmeklētājs no vienas rūtiņas (telpas) var pāriet uz citu rūtiņu (telpu), ja tām ir kopīga mala;
apmeklētājs maršruta laikā apmeklē katru rūtiņu (telpu) tieši vienu reizi;
maršruts beidzas rūtiņā (telpā), kas atrodas pie taisnstūra malas blakus maršruta sākuma rūtiņai (telpai).

Vai muzeja vadītājs var izveidot šādu maršrutu?