2.2.3.0.0. Orientēti grafi
Orientēti grafi (grafa šķautnēm ir noteikts virziens, ko apzīmē, piemēram, ar bultiņu).
LV.AMO.2024.8.3
Trīs burvji rituālā spēj pārveidot skaitļus, bet katrs no burvjiem prot tikai vienu burvestību:
- pirmais burvis spēj atņemt no jebkura skaitḷa \(1\);
- otrais burvis spēj izdalīt jebkuru skaitli ar \(2\);
- trešais burvis spēj reizināt jebkuru skaitli ar \(3\).
Lai pārveidotu skaitli, burvji var pielietot savas burvestības jebkurā secībā, pat izlaižot citus burvjus. Bet katrs burvis savu burvestību katrā rituālā drīkst izmantot tikai \(5\) reizes, un starprezultātam jābūt veselam skaitlim, kas nepārsniedz \(9\). Vai burvji rituālā no skaitliem \(3,8,9,2,4\) var iegūt (A) \(3,3,3,3,3\); (B) \(5,5,5,5,5\)?
LV.AMO.2017.9.4
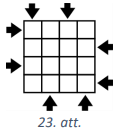
(A) Pierādi, ka dotajā \(4 \times 4\) rūtiņu laukumā (skat. 23.att.) nevar ierakstīt \(16\) dažādus naturālus skaitļus tā, lai katrā rūtiņā būtu ierakstīts viens skaitlis un katrā rindā un katrā kolonnā skaitļi pieaugtu bultiņas norādītajā virzienā.
(B) Kāds mazākais bultiņu skaits jāapvērš pretējā virzienā, lai skaitļus varētu izvietot saskaņā ar uzdevuma nosacījumiem?
LV.AMO.2018.9.4
Atrast lielāko naturālo skaitli, kas dalās ar \(7\), kura ciparu summa ir \(100\) un kuram neviens cipars nav \(0\).