4.1.0.0.0. Skaitļu dalāmība
Uzdevumi par dalāmības attiecību, saliktu skaitļu un pirmskaitļu pazīšana. Uzdevumi par LKD un MKD; fiksēta skaitļa visu dalītāju režģis. Skaitļa visu dalītāju skaita un summas formulas.
LV.AMO.2022B.5.1
What is the smallest positive integer that uses only the digits \(0\) and \(2\) in its notation and is divisible by \(15\)?
LV.AMO.2022B.5.1
Kāds ir mazākais naturālais skaitlis, kura pierakstā izmantoti tikai cipari \(0\) un \(2\) un kurš dalās ar \(15\)?
LV.AMO.2022B.5.1
What is the smallest positive integer that uses only the digits \(0\) and \(2\) in its notation and is divisible by \(15\)?
LV.AMO.2022B.5.1
Kāds ir mazākais naturālais skaitlis, kura pierakstā izmantoti tikai cipari \(0\) un \(2\) un kurš dalās ar \(15\)?
LV.AMO.2022B.5.3
\(250\) tickets were made for the theatre performance and at least half of them were sold. It is known that exactly a third of the audience were schoolchildren, exactly one fifth of the audience were students and exactly one-seventh were retirees. How many tickets were sold?
LV.AMO.2022B.5.3
Uz teātra izrādi tika izgatavotas \(250\) biļetes un vismaz puse no biļetēm tika pārdotas. Zināms, ka tieši trešdaļa no skatītājiem bija skolēni, tieši piektdaļa – studenti un tieši septītdaļa – pensionāri. Cik biļetes tika pārdotas?
LV.AMO.2022B.5.3
\(250\) tickets were made for the theatre performance and at least half of them were sold. It is known that exactly a third of the audience were schoolchildren, exactly one fifth of the audience were students and exactly one-seventh were retirees. How many tickets were sold?
LV.AMO.2022B.5.3
Uz teātra izrādi tika izgatavotas \(250\) biļetes un vismaz puse no biļetēm tika pārdotas. Zināms, ka tieši trešdaļa no skatītājiem bija skolēni, tieši piektdaļa – studenti un tieši septītdaļa – pensionāri. Cik biļetes tika pārdotas?
LV.AMO.2003.6.1
Šodien pulkst. \(12^{00}\) divi pulksteņi ar parastu ciparnīcu rādīja pareizu laiku. Pirmais pulkstenis katru dienu steidzas par \(4\) minūtēm, otrais pulkstenis katru dienu atpaliek par \(6\) minūtēm. Pēc cik dienām pirmo reizi pulkst. \(12^{00}\) abi pulksteņi atkal rādīs pareizu laiku?
LV.AMO.2022B.6.1
All positive integers from \(1\) to \(2022\) are written on a piece of paper, each appearing once. First, Amanda circled all the numbers divisible by \(3\) in red. She then circled all the numbers divisible by \(5\) in blue. Finally, she circled all the numbers divisible by \(7\) in green. How many numbers are circled with at least two different colors?
LV.AMO.2022B.6.1
Uz papīra lapas uzrakstīti visi naturālie skaitļi no \(1\) līdz \(2022\) (katrs vienu reizi). Vispirms Amanda ar sarkanu zīmuli apvilka visus skaitļus, kas dalās ar \(3\). Tad viņa ar zilu zīmuli apvilka visus skaitļus, kas dalās ar \(5\). Un visbeidzot viņa ar zaļu zīmuli apvilka visus skaitļus, kas dalās ar \(7\). Cik ir tādu skaitļu, kas ir apvilkti ar vismaz divām dažādām krāsām?
LV.AMO.2004.7.3
Kādam mazākajam naturālajamam \(n\) visas daļas \(\frac{5}{n+7}, \frac{6}{n+8}, \frac{7}{n+9}, \ldots, \frac{35}{n+37}, \frac{36}{n+38}\) ir nesaīsināmas?
LV.AMO.2005.7.4
Triju veselu pozitīvu skaitļu summa ir \(407\). Ar kādu lielāko daudzumu nuļļu var beigties šo skaitļu reizinājums?
LV.AMO.2008.7.2
Dots, ka \(x\) un \(y\) - tādi naturāli skaitļi, ka \(x \cdot y=10^{12}\). Vai var būt, ka ne \(x\), ne \(y\) nesatur savā pierakstā nevienu ciparu \(0\)?
LV.AMO.2011.7.3
Atrodi naturālu skaitli, kuru, dalot ar \(2010\), atlikumā iegūst \(13\), bet, dalot ar \(2011\), atlikumā iegūst \(3\).
LV.AMO.2013.7.3
Pierādīt, ka skaitlis \(1234567891011\ldots175176\) (pēc kārtas uzrakstīti visi naturālie skaitļi no \(1\) līdz \(176\)) nav naturāla skaitļa kvadrāts. (Skaitļa kvadrāts ir skaitļa reizinājums pašam ar sevi.)
LV.AMO.2013.7.3
Pierādīt, ka skaitlis \(1234567891011\ldots175176\) (pēc kārtas uzrakstīti visi naturālie skaitļi no \(1\) līdz \(176\)) nav naturāla skaitļa kvadrāts. (Skaitļa kvadrāts ir skaitļa reizinājums pašam ar sevi.)
LV.AMO.2015.7.3
(A) Atrast tādu naturālu skaitli, kura ciparu summa ir \(13\), pēdējie divi cipari ir \(13\) un kurš dalās ar \(13\).
(B) Vai var atrast tādu naturālu skaitli, kura ciparu summa ir \(11\), pēdējie divi cipari ir \(11\) un kurš dalās ar \(11\)?
LV.AMO.2015.7.3
(A) Atrast tādu naturālu skaitli, kura ciparu summa ir \(13\), pēdējie divi cipari ir \(13\) un kurš dalās ar \(13\).
(B) Vai var atrast tādu naturālu skaitli, kura ciparu summa ir \(11\), pēdējie divi cipari ir \(11\) un kurš dalās ar \(11\)?
LV.AMO.2015.7.3
(A) Atrast tādu naturālu skaitli, kura ciparu summa ir \(13\), pēdējie divi cipari ir \(13\) un kurš dalās ar \(13\).
(B) Vai var atrast tādu naturālu skaitli, kura ciparu summa ir \(11\), pēdējie divi cipari ir \(11\) un kurš dalās ar \(11\)?
LV.AMO.2019.7.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā septiņu naturālu skaitļu reizinājumu tā, lai to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2019.7.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā septiņu naturālu skaitļu reizinājumu tā, lai to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2022A.7.2
Karlsonam ir \(30\) milzīgi tortes gabali. Viņš izvēlas trīs gabalus un sagriež katru no tiem vai nu \(3\), vai \(5\) mazākos gabalos (visus izvēlētos gabalus sagriež vienādā skaitā mazāku gabalu). Tad viņš atkal izvēlas kādus \(3\) gabalus un sagriež katru no tiem vai nu \(3\), vai \(5\) mazākos gabalos (visus izvēlētos gabalus sagriež vienādā skaitā gabalu). Vai, atkārtoti izpildot šādas darbības, Karlsons var iegūt tieši \(2000\) tortes gabalus?
LV.AMO.2022A.7.4
Elektroniskais pulkstenis rāda stundu skaitu (vesels skaitlis robežās no \(0\) līdz \(23\)) un minūšu skaitu (vesels skaitlis robežās no \(0\) līdz \(59\)). Noteikt, cik reižu diennaktī stundu skaita un minūšu skaita starpība dalās ar \(7\).
LV.AMO.2022A.7.5
Trijzemē apgrozībā ir trīs veidu monētas: \(2\) centi, \(5\) centi un vēl viena. Zināms, ka gan trijkāji, kas maksā \(13\) centus, gan trīsriteni, kas maksā \(19\) centus, var nopirkt, maksājot tieši ar trīs monētām. Kāda ir Trijzemes trešās monētas vērtība? Atrodi visus iespējamos variantus un pamato, ka citu nav!
LV.AMO.2022B.7.1
The following text was written on the board: \(A869B\). Each of the letters \(A\) and \(B\) must be replaced by one digit (they may or may not be the same) so that the resulting five-digit number is divisible by \(15\). In how many ways can you do this?
LV.AMO.2022B.7.1
Uz tāfeles bija uzrakstīts šāds teksts: \(A869B\). Katrs no burtiem \(A\) un \(B\) jāaizstāj ar vienu ciparu (tie var būt arī vienādi) tā, lai iegūtais piecciparu skaitlis dalītos ar \(15\). Cik dažādos veidos to var izdarīt?
LV.AMO.2022B.7.1
The following text was written on the board: \(A869B\). Each of the letters \(A\) and \(B\) must be replaced by one digit (they may or may not be the same) so that the resulting five-digit number is divisible by \(15\). In how many ways can you do this?
LV.AMO.2022B.7.1
Uz tāfeles bija uzrakstīts šāds teksts: \(A869B\). Katrs no burtiem \(A\) un \(B\) jāaizstāj ar vienu ciparu (tie var būt arī vienādi) tā, lai iegūtais piecciparu skaitlis dalītos ar \(15\). Cik dažādos veidos to var izdarīt?
LV.AMO.2023.7.2
Kāds ir lielākais iespējamais septiņciparu skaitlis, kuram vienlaicīgi izpildās šādi nosacījumi:
- tas dalās ar \(12\);
- skaitļa pirmais cipars ir tāds pats kā pēdējais cipars;
- skaitļa 2., 4. un 6. cipars ir vienādi un tie ir divas reizes lielāki nekā pirmais cipars;
- skaitļa trešais cipars ir tāds pats kā piektais cipars?
LV.AMO.2023.7.5
Uz palodzes sēž vairākas bizbizmārītes, katrai no tām uz muguras ir vai nu divi punktiņi, vai septiņi punktiņi. Tās bizbizmārītes, kurām uz muguras ir septiņi punktiņi, vienmēr saka patiesību, bet tās bizbizmārītes, kurām uz muguras ir divi punktiņi, vienmēr melo. Katra bizbizmārīte izteicās:
- pirmā bizbizmārīte teica: "punktiņu skaits uz muguras mums visām ir vienāds";
- otrā teica: "mums visām kopā uz muguras ir \(42\) punktiņi";
- trešā teica: "nē, mums visām kopā uz muguras ir \(32\) punktiņi";
- katra no atlikušajām bizbizmārītēm teica: "no pirmajām trijām bizbizmārītēm tieši viena teica patiesību".
Cik bizbizmārīšu sēž uz palodzes?
LV.AMO.2024.7.5
Anita, Maija, Ināra un Sandra uzstājās koncertā. Katru dziesmu dziedāja 3 meitenes. Cik dziesmu meitenes nodziedāja pavisam, ja Anita dziedāja 7 dziesmas (vairāk nekā jebkura cita meitene), bet Sandra dziedāja 4 dziesmas (mazāk nekā jebkura cita meitene)?
LV.NOL.2007.7.1
Kurus naturālos skaitļus \(n\) var izsacīt formā \(n=\frac{x}{y}\), kur \(x=a^{5},\ y=b^{3}\), \(a\) un \(b\) - naturāli skaitļi?
LV.NOL.2008.7.1
Kurus naturālos skaitļus \(n\) var izsacīt formā \(n=\frac{x}{y}\), kur \(x=a^{3},\ y=b^{4},\ a\) un \(b\) - naturāli skaitļi?
LV.NOL.2009.7.1
Kurus naturālos skaitļus \(n\) var izsacīt formā \(n=\frac{x}{y}\), kur \(x=a^{3}, y=b^{5}\), \(a\) un \(b\) naturāli skaitļi?
LV.NOL.2010.7.3
Cik ir tādu naturālu skaitļu \(x\) robežās no \(1\) līdz \(2010\) ieskaitot, ka \((x+1)(x+2)(x+3)\) dalās ar \(343\)?
LV.NOL.2011.7.2
Cik ir tādu naturālu skaitļu \(n\) no \(1\) līdz \(2011\) ieskaitot, ka skaitlis \((n+1)(n+2)(n+3)\) dalās ar \(125\)?
LV.NOL.2012.7.4
Pierādīt, ka \(1004041\) nav pirmskaitlis.
LV.NOL.2013.7.2
Cik starp pirmajiem \(2013\) naturālajiem skaitļiem ir tādu skaitļu \(x\), ka skaitlis \(x(x+1)(x+2)\) dalās ar \(111\)?
LV.NOL.2013.7.2
Cik starp pirmajiem \(2013\) naturālajiem skaitļiem ir tādu skaitļu \(x\), ka skaitlis \(x(x+1)(x+2)\) dalās ar \(111\)?
LV.NOL.2014.7.3
Cik starp pirmajiem \(2014\) naturālajiem skaitļiem ir tādu skaitļu \(x\), ka skaitlis \(x(x+1)(x+2)\) dalās ar \(87\)?
LV.NOL.2014.7.3
Cik starp pirmajiem \(2014\) naturālajiem skaitļiem ir tādu skaitļu \(x\), ka skaitlis \(x(x+1)(x+2)\) dalās ar \(87\)?
LV.NOL.2016.7.2
Dots naturāls skaitlis, kas dalās ar \(99\) un kura pēdējais cipars nav \(0\). Pierādi, ka, uzrakstot šī skaitļa ciparus pretējā secībā, arī iegūst skaitli, kas dalās ar \(99\).
LV.NOL.2016.7.2
Dots naturāls skaitlis, kas dalās ar \(99\) un kura pēdējais cipars nav \(0\). Pierādi, ka, uzrakstot šī skaitļa ciparus pretējā secībā, arī iegūst skaitli, kas dalās ar \(99\).
LV.NOL.2016.7.2
Dots naturāls skaitlis, kas dalās ar \(99\) un kura pēdējais cipars nav \(0\). Pierādi, ka, uzrakstot šī skaitļa ciparus pretējā secībā, arī iegūst skaitli, kas dalās ar \(99\).
LV.AMO.2003.8.3
Kādā lielākajā daudzumā dažādu naturālu saskaitāmo, kas visi lielāki par \(1\), var sadalīt skaitli \(56\) tā, lai katru divu saskaitāmo lielākais kopīgais dalītājs būtu \(1\)?
LV.AMO.2004.8.5
Virknē augošā kārtībā izrakstīti naturālie skaitļi no \(1\) līdz \(2004\) ieskaitot, katrs vienu reizi. Izsvītrojam no tās skaitļus, kas atrodas \(1.,\ 4.,\ 7.,\ 10.,\ \ldots\) vietās. No palikušās virknes atkal izsvītrojam skaitļus, kas tajā atrodas \(1.,\ 4.,\ 7.,\ \ldots\) vietās. Ar iegūto virkni rīkojamies tāpat, utt., kamēr paliek neizsvītrots viens skaitlis. Kurš tas ir?
LV.AMO.2006.8.3
Naturāla skaitļa \(x\) ciparu summu apzīmēsim ar \(S(x)\). Pieņemsim, ka \(n\) - tāds naturāls skaitlis, kam vienlaicīgi izpildās īpašības \(S(n)=10\) un \(S(5n)=5\).
(A) atrodiet kaut vienu tādu skaitli,
(B) vai tādu skaitļu ir bezgalīgi daudz?
(C) vai kāds no tādiem skaitļiem ir nepāra?
LV.AMO.2016.8.3
Zināms, ka skaitlis dalās ar \(2016\) un ka visi tā cipari ir dažādi. Kāds ir lielākais ciparu skaits, kas var būt šajā skaitlī?
LV.AMO.2016.8.3
Zināms, ka skaitlis dalās ar \(2016\) un ka visi tā cipari ir dažādi. Kāds ir lielākais ciparu skaits, kas var būt šajā skaitlī?
LV.AMO.2016.8.3
Zināms, ka skaitlis dalās ar \(2016\) un ka visi tā cipari ir dažādi. Kāds ir lielākais ciparu skaits, kas var būt šajā skaitlī?
LV.AMO.2019.8.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā sešu naturālu skaitļu reizinājumu tā, ka neviens no tiem nav mazāks kā \(10\) un to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2019.8.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā sešu naturālu skaitļu reizinājumu tā, ka neviens no tiem nav mazāks kā \(10\) un to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2022A.8.2
Kādā dienā Karlsons uzlika uz galda \(44\) kūciņas. Lai būtu jautrāk, Karlsons izdomāja, ka vienā piegājienā viņš apēdīs vai nu \(5\) kūciņas, vai arī \(10\) kūciņas. Ja Karlsons apēda \(5\) kūciņas, tad Brālītis uzreiz uz galda uzlika \(9\) kūciņas. Ja Karlsons apēda \(10\) kūciņas, tad Brālītis uzreiz uz galda uzlika \(2\) kūciņas. Vai iespējams, ka kādā brīdī uz galda bija tieši \(2022\) kūciņas?
LV.AMO.2022A.8.4
Māris iedomājās naturālu skaitli \(n\). Pēc tam viņš izvēlējās vienu skaitļa \(n\) dalītāju, pareizināja to ar \(4\) un iegūto reizinājumu atņēma no dotā skaitļa \(n\), iegūstot vērtību \(11\). Kāda varēja būt \(n\) vērtība? Atrodi visus variantus un pamato, ka citu nav!
LV.AMO.2022B.8.1
The following text was written on the board: \(N597M\). Each of the letters \(N\) and \(M\) should be replaced by a digit (they may or may not be the same) so that the resulting five digit number is divisible by \(12\). In how many ways can you do this?
LV.AMO.2022B.8.1
Uz tāfeles bija uzrakstīts šāds teksts: \(N597M\). Katrs no burtiem \(N\) un \(M\) jāaizstāj ar vienu ciparu (tie var būt arī vienādi) tā, lai iegūtais piecciparu skaitlis dalītos ar \(12\). Cik dažādos veidos to var izdarīt?
LV.AMO.2022B.8.1
The following text was written on the board: \(N597M\). Each of the letters \(N\) and \(M\) should be replaced by a digit (they may or may not be the same) so that the resulting five digit number is divisible by \(12\). In how many ways can you do this?
LV.AMO.2022B.8.1
Uz tāfeles bija uzrakstīts šāds teksts: \(N597M\). Katrs no burtiem \(N\) un \(M\) jāaizstāj ar vienu ciparu (tie var būt arī vienādi) tā, lai iegūtais piecciparu skaitlis dalītos ar \(12\). Cik dažādos veidos to var izdarīt?
LV.AMO.2023.8.2
Trīsciparu skaitļa \(x\) ciparu summa ir \(12\). Ja šim skaitlim nodzēš pēdējo ciparu, tad atlikušais divciparu skaitlis dalās ar \(9\). Zināms, ka skaitlis \(x\) ir par \(99\) lielāks nekā trīsciparu skaitlis, ko iegūst, uzrakstot tā ciparus pretējā secībā. Kāds var būt skaitlis \(x\)?
LV.AMO.2023.8.5
Uz palodzes sēž vairākas bizbizmārītes, katrai no tām uz muguras ir vai nu trīs punktiņi, vai astoņi punktiņi. Tās bizbizmārītes, kurām uz muguras ir astoņi punktiņi, vienmēr saka patiesību, bet tās bizbizmārītes, kurām uz muguras ir trīs punktiņi, vienmēr melo. Katra bizbizmārīte izteicās:
- pirmā bizbizmārīte teica: "punktiņu skaits uz muguras mums visām ir vienāds";
- otrā teica: "mums visām kopā uz muguras ir \(38\) punktiņi";
- trešā teica: "nē, mums visām kopā uz muguras ir \(48\) punktiņi";
- katra no atlikušajām bizbizmārītēm teica: "no pirmajām trijām bizbizmārītēm tieši viena teica patiesību".
Cik bizbizmārītes sēž uz palodzes?
LV.NOL.2005.8.3
Andris iedomājās patvaļīgu naturālu skaitli \(n\). Juris ar vienu gājienu var pateikt Andrim piecus dažādus naturālus skaitļus \(x_{1},\ x_{2},\ x_{3},\ x_{4},\ x_{5}\), un Andris pateiks Jurim vienu no skaitļiem \(nx_{1},\ nx_{2},\ nx_{3},\ nx_{4},\ nx_{5}\) (bet nepaskaidros, kura reizinājuma vērtību viņš saka).
Ar kādu mazāko jautājumu skaitu Juris var noteikti noskaidrot \(n\)?
LV.NOL.2007.8.4
Atrast mazāko naturālo skaitli, kas dalās ar katru no kaut kādiem \(12\) pēc kārtas ņemtiem naturāliem skaitļiem.
LV.NOL.2007.8.4
Atrast mazāko naturālo skaitli, kas dalās ar katru no kaut kādiem \(12\) pēc kārtas ņemtiem naturāliem skaitļiem.
LV.NOL.2010.8.3
Četrciparu skaitlim pārlika ciparus citā kārtībā. Pierādīt: sākotnējā un iegūtā skaitļa starpība dalās ar \(9\).
LV.NOL.2010.8.3
Četrciparu skaitlim pārlika ciparus citā kārtībā. Pierādīt: sākotnējā un iegūtā skaitļa starpība dalās ar \(9\).
LV.NOL.2011.8.1
Piecciparu skaitlis \(B\) ir iegūts no mazāka piecciparu skaitļa \(A\), samainot vietām tā ciparus. Pierādīt, ka \(B-A\) dalās ar \(9\).
LV.NOL.2011.8.1
Piecciparu skaitlis \(B\) ir iegūts no mazāka piecciparu skaitļa \(A\), samainot vietām tā ciparus. Pierādīt, ka \(B-A\) dalās ar \(9\).
LV.NOL.2012.8.3
Vai naturāla skaitļa ciparu reizinājums var būt skaitlis \(\overline{aabbcc}\)? (Pieraksts \(\overline{kmn}\) nozīmē, ka skaitlī ir \(k\) simti, \(m\) desmiti un \(n\) vieni.)
LV.NOL.2016.8.2
Karlīna uzrakstīja divus skaitļus, kuru pierakstā nav izmantots cipars \(0\). Katru ciparu viņa aizstāja ar burtu: dažādus ciparus - ar dažādiem burtiem, vienādus - ar vienādiem. Viens no uzrakstītajiem skaitļiem \(DUBĻUNNN\) dalās ar \(104\). Pierādi, ka otrais skaitlis \(BURBUĻUVANNA\) nedalās ar \(56\).
LV.AMO.2003.9.3
Noskaidrot, kādiem dažādiem pirmskaitļiem \(p_{1},\ p_{2},\ \ldots,\ p_{n}\) pastāv īpašība: \(p_{1}p_{2}p_{3} \ldots p_{n}\) dalās ar \(\left(p_{1}-1\right)\left(p_{2}-1\right) \ldots \left(p_{n}-1\right)\).
LV.AMO.2022A.9.2
Sākumā uz tāfeles uzrakstīts skaitlis \(2112\). Ar to atļauts veikt šādas darbības:
- patvaļīgi mainīt uzrakstīto ciparu secību;
- ja skaitļa pēdējie divi cipari ir \(12\), tos drīkst nodzēst;
- ciparu grupu "\(21\)" var aizstāt ar "\(22233\)"
- ciparu grupu "\(223\)" var aizstāt ar "\(1\)".
Vai, atkārtojot vairākus šādus gājienus, ir iespējams iegūt skaitli \(212\)?
LV.AMO.2022A.9.2
Sākumā uz tāfeles uzrakstīts skaitlis \(2112\). Ar to atļauts veikt šādas darbības:
- patvaļīgi mainīt uzrakstīto ciparu secību;
- ja skaitļa pēdējie divi cipari ir \(12\), tos drīkst nodzēst;
- ciparu grupu "\(21\)" var aizstāt ar "\(22233\)"
- ciparu grupu "\(223\)" var aizstāt ar "\(1\)".
Vai, atkārtojot vairākus šādus gājienus, ir iespējams iegūt skaitli \(212\)?
LV.AMO.2022B.9.1
How many four-digit numbers \(\overline{ABBA}\) are there that are divisible by \(99\)? (The same letters are replaced by the same digits, but different letters may or may not be the same.)
LV.AMO.2022B.9.1
Cik ir tādu četrciparu skaitļu \(\overline{ABBA}\), kas dalās ar \(99\)? (Vienādiem burtiem atbilst vienādi cipari, dažādiem burtiem var atbilst arī vienādi cipari.)
LV.AMO.2022B.9.1
How many four-digit numbers \(\overline{ABBA}\) are there that are divisible by \(99\)? (The same letters are replaced by the same digits, but different letters may or may not be the same.)
LV.AMO.2022B.9.1
Cik ir tādu četrciparu skaitļu \(\overline{ABBA}\), kas dalās ar \(99\)? (Vienādiem burtiem atbilst vienādi cipari, dažādiem burtiem var atbilst arī vienādi cipari.)
LV.AMO.2024.9.5
Ingai ir tālrunis ar šādu pogu izkārtojumu:
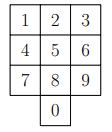
Viṇas draudzenes Zanes deviņciparu tālruņa numuram ir šādas īpašības:
- visi Zanes tālruņa numura cipari ir atšk̦irīgi;
- pirmie četri cipari ir sakārtoti augošā secībā un to attiecīgo pogu centri veido kvadrātu;
- pēdējo četru ciparu pogu centri arı̄ veido kvadrātu;
- Zanes tālruņa numurs dalās ar \(15\).
Cik ir tādu deviņciparu tālruņa numuru, kas varētu būt Zanes tālruņa numurs?
LV.AMO.2024.9.5
Ingai ir tālrunis ar šādu pogu izkārtojumu:

Viṇas draudzenes Zanes deviņciparu tālruņa numuram ir šādas īpašības:
- visi Zanes tālruņa numura cipari ir atšk̦irīgi;
- pirmie četri cipari ir sakārtoti augošā secībā un to attiecīgo pogu centri veido kvadrātu;
- pēdējo četru ciparu pogu centri arı̄ veido kvadrātu;
- Zanes tālruņa numurs dalās ar \(15\).
Cik ir tādu deviņciparu tālruņa numuru, kas varētu būt Zanes tālruņa numurs?
LV.AMO.2016.10.2
Vai var atrast tādus veselus skaitļus \(x, y\) un \(z\), ka \(x^{3}-2016xyz=120\) ?
LV.AMO.2017.10.5
Pierādīt, ja no trim naturāliem skaitļiem \(n\); \(n+11\) un \(n+22\) divi ir pirmskaitļi, tad trešais skaitlis dalās ar \(6\).
LV.AMO.2017.10.5
Pierādīt, ja no trim naturāliem skaitļiem \(n\); \(n+11\) un \(n+22\) divi ir pirmskaitļi, tad trešais skaitlis dalās ar \(6\).
LV.AMO.2018.10.4
Pierādīt, ja \(x\) - naturāls skaitlis, tad \(x^{8}-x^{2}\) dalās ar \(252\).
LV.AMO.2018.10.4
Pierādīt, ja \(x\) - naturāls skaitlis, tad \(x^{8}-x^{2}\) dalās ar \(252\).
LV.AMO.2022B.10.2
Consider \(n\) consecutive positive integers. Can we divide them into two groups so that the sum of the numbers in each group is a prime number if (A) \(n = 8\), (B) \(n = 10\)? Each group must contain at least \(2\) numbers.
LV.AMO.2022B.10.2
Apskatām \(n\) pēc kārtas ņemtus naturālus skaitļus. Vai var gadīties, ka tos var sadalīt divās grupās tā, ka katras grupas skaitļu summa ir pirmskaitlis, ja (A) \(n = 8\), (B) \(n = 10\)? Katrā grupā jābūt vismaz \(2\) skaitļiem.
LV.NOL.2008.10.1
Atrodiet mazāko naturālo skaitli, ko var izsacīt gan kā \(15\), gan kā \(16\), gan kā \(17\) pēc kārtas ņemtu naturālu skaitļu summu.
LV.NOL.2010.10.2
Dots, ka \(a\) un \(b\) ir naturāli skaitļi, \(a^{2}\) dalās ar \(b\) un \(b^{2}\) dalās ar \(a\). Pierādīt, ka \((a-b)^{3}\) dalās ar \(a \cdot b\). Vai noteikti \((a-b)^{2}\) dalās ar \(a \cdot b\)?
LV.NOL.2012.10.3
Doti seši pēc kārtas sekojoši naturāli skaitļi. Pierādīt, ka var atrast tādu pirmskaitli \(p\), ka tieši viens no dotajiem skaitļiem dalās ar \(p\).
LV.NOL.2014.10.2
Pierādīt, ka, izvēloties \(52\) no aritmētiskās progresijas \(1,\ 4,\ 7,\ 10,\ \ldots\) locekļiem, kas nepārsniedz \(300\), vienmēr starp šiem skaitļiem var atrast divus skaitļus, kuru summa ir \(302\).
LV.NOL.2015.10.2
Ar naturālu skaitli atļauts veikt šādas darbības:
- pieskaitīt \(6\);
- dalīt ar \(4\), ja skaitlis dalās ar \(4\);
- mainīt vietām skaitļa ciparus (skaitļa sākumā nedrīkst atrasties nulle).
Vai, atkārtoti izpildot šīs darbības, no skaitļa \(30\) var iegūt skaitli \(2015\)?
LV.NOL.2017.10.5
Desmitciparu skaitlī vienādus ciparus aizvietojot ar vienādiem burtiem, bet dažādus- ar dažādiem, ieguva vārdu MATEMĀTIKA (īsais " \(A\) " un garais " \(Ā\) " aizstāj atšķirīgus ciparus). Papildus zināms, ka skaitlis \(\overline{MA}\) dalās ar \(2\), \(\overline{MAT}\)- ar \(3\), \(\overline{MATE}\)- ar \(4\), \(\overline{\text { MATEM }}\)- ar \(5\), \(\overline{MATEM \bar{A}}\)- ar \(6\), \(\overline{MATEM \bar{A}T}\)- ar \(7\), \(\overline{MATEM \bar{A}TI}\)- ar \(8\), \(\overline{MATEM \bar{A}TIK}\)- ar \(9\), \(\overline{MATEM \bar{A}TIKA}\)- ar \(10\). Noteikt, kāds bija sākotnējais desmitciparu skaitlis!
LV.NOL.2017.10.5
Desmitciparu skaitlī vienādus ciparus aizvietojot ar vienādiem burtiem, bet dažādus- ar dažādiem, ieguva vārdu MATEMĀTIKA (īsais " \(A\) " un garais " \(Ā\) " aizstāj atšķirīgus ciparus). Papildus zināms, ka skaitlis \(\overline{MA}\) dalās ar \(2\), \(\overline{MAT}\)- ar \(3\), \(\overline{MATE}\)- ar \(4\), \(\overline{\text { MATEM }}\)- ar \(5\), \(\overline{MATEM \bar{A}}\)- ar \(6\), \(\overline{MATEM \bar{A}T}\)- ar \(7\), \(\overline{MATEM \bar{A}TI}\)- ar \(8\), \(\overline{MATEM \bar{A}TIK}\)- ar \(9\), \(\overline{MATEM \bar{A}TIKA}\)- ar \(10\). Noteikt, kāds bija sākotnējais desmitciparu skaitlis!
LV.NOL.2017.10.5
Desmitciparu skaitlī vienādus ciparus aizvietojot ar vienādiem burtiem, bet dažādus- ar dažādiem, ieguva vārdu MATEMĀTIKA (īsais " \(A\) " un garais " \(Ā\) " aizstāj atšķirīgus ciparus). Papildus zināms, ka skaitlis \(\overline{MA}\) dalās ar \(2\), \(\overline{MAT}\)- ar \(3\), \(\overline{MATE}\)- ar \(4\), \(\overline{\text { MATEM }}\)- ar \(5\), \(\overline{MATEM \bar{A}}\)- ar \(6\), \(\overline{MATEM \bar{A}T}\)- ar \(7\), \(\overline{MATEM \bar{A}TI}\)- ar \(8\), \(\overline{MATEM \bar{A}TIK}\)- ar \(9\), \(\overline{MATEM \bar{A}TIKA}\)- ar \(10\). Noteikt, kāds bija sākotnējais desmitciparu skaitlis!
LV.NOL.2017.10.5
Desmitciparu skaitlī vienādus ciparus aizvietojot ar vienādiem burtiem, bet dažādus- ar dažādiem, ieguva vārdu MATEMĀTIKA (īsais " \(A\) " un garais " \(Ā\) " aizstāj atšķirīgus ciparus). Papildus zināms, ka skaitlis \(\overline{MA}\) dalās ar \(2\), \(\overline{MAT}\)- ar \(3\), \(\overline{MATE}\)- ar \(4\), \(\overline{\text { MATEM }}\)- ar \(5\), \(\overline{MATEM \bar{A}}\)- ar \(6\), \(\overline{MATEM \bar{A}T}\)- ar \(7\), \(\overline{MATEM \bar{A}TI}\)- ar \(8\), \(\overline{MATEM \bar{A}TIK}\)- ar \(9\), \(\overline{MATEM \bar{A}TIKA}\)- ar \(10\). Noteikt, kāds bija sākotnējais desmitciparu skaitlis!
LV.NOL.2018.10.4
No cipariem \(1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9\), katru izmantojot divas reizes, izveidoti trīs sešciparu skaitļi. Ar kādu lielāko nuļļu skaitu var beigties trīs izveidoto skaitļu summa?
LV.NOL.2019.10.5
Atrast visus pirmskaitļu pārus \((m, n)\), kuriem \(20m+18n=2018\).
LV.VOL.2014.10.3
Ir pieejams neierobežots daudzums \(7\) un \(13\) centu pastmarku, kuras izmanto pasta sūtījumu apmaksāšanai. Diemžēl dažas summas nav iespējams apmaksāt tikai ar šīm pastmarkām (piemēram, ja sūtījums maksā \(6,\ 8\) vai \(25\) centus). Kāda ir lielākā summa, kuru nav iespējams apmaksāt izmantojot tikai šīs pastmarkas?
LV.VOL.2015.10.2
Pierādīt, ka katram naturālam \(n\) izteiksme \(3n^{5}+5n^{4}-8n\) dalās ar \(10\).
LV.VOL.2017.10.2
Dots pirmskaitlis, kas satur vismaz \(4\) dažādus ciparus. Pierādīt, ka tā ciparus var pārkārtot citā secībā tā, lai jauniegūtais skaitlis nebūtu pirmskaitlis!
LV.VOL.2018.10.3
Skaitļus \(a,\ b,\ c\) sauksim par skaistu trijnieku, ja tiem piemīt šādas īpašības:
- tie ir trīs pēc kārtas esoši naturāli skaitļi;
- katrs no tiem dalās ar savu ciparu summu.
Piemēram, skaists trijnieks ir \(8,\ 9,\ 10\).
(A) Atrast tādu skaistu trijnieku, kurā mazākais skaitlis ir lielāks nekā \(10\).
(B) Pierādīt, ka eksistē bezgalīgi daudz skaistu trijnieku!
LV.VOL.2018.10.3
Skaitļus \(a,\ b,\ c\) sauksim par skaistu trijnieku, ja tiem piemīt šādas īpašības:
- tie ir trīs pēc kārtas esoši naturāli skaitļi;
- katrs no tiem dalās ar savu ciparu summu.
Piemēram, skaists trijnieks ir \(8,\ 9,\ 10\).
(A) Atrast tādu skaistu trijnieku, kurā mazākais skaitlis ir lielāks nekā \(10\).
(B) Pierādīt, ka eksistē bezgalīgi daudz skaistu trijnieku!
LV.VOL.2019.10.3
Pierādīt, ka nevienai naturālai \(n\) vērtībai izteiksmes \(13^{n}+7^{n}+2019\) vērtība nav naturāla skaitļa kvadrāts!