Tēma

2.1.0.0.0. Objektu skaitīšana

Noskaidrot, cik veidos var izvēlēties pārstāvjus, cik veidos var izdarīt kādas specifiskas darbības. Noteikt, cik veidos var sakārtot kādas kopas vai apakškopas elementus.

LV.AMO.2011.5.5

Kvadrātā ar izmēriem \(7 \times 7\) rūtiņas jāizvieto \(n\) "stūrīšus" (2.zīm. attēlotās figūras) tā, lai tajā vairāk nevarētu ievietot nevienu citu šādu "stūrīti". (Stūrīšu malām jāiet pa rūtiņu malām. Stūrīši var arī būt pagriezti citādāk.)

Parādi, kā to var izdarīt, ja
(A) \(n=9\);
(B) \(n=8\).

LV.AMO.2003.6.2

Kvadrāts sastāv no \(n \times n\) rūtiņām; viena stūra rūtiņa izgriezta. Rūtiņas malas garums ir \(1\). Atlikušo daļu jāsadala taisnstūros ar izmēriem \(1 \times 2\) tā, lai pusei no tiem garākā mala ietu vienā virzienā, bet pusei - otrā. Vai to var izdarīt, ja (A) \(n=5\), (B) \(n=7\)?

LV.AMO.2022B.6.1

All positive integers from \(1\) to \(2022\) are written on a piece of paper, each appearing once. First, Amanda circled all the numbers divisible by \(3\) in red. She then circled all the numbers divisible by \(5\) in blue. Finally, she circled all the numbers divisible by \(7\) in green. How many numbers are circled with at least two different colors?

LV.AMO.2022B.6.1

Uz papīra lapas uzrakstīti visi naturālie skaitļi no \(1\) līdz \(2022\) (katrs vienu reizi). Vispirms Amanda ar sarkanu zīmuli apvilka visus skaitļus, kas dalās ar \(3\). Tad viņa ar zilu zīmuli apvilka visus skaitļus, kas dalās ar \(5\). Un visbeidzot viņa ar zaļu zīmuli apvilka visus skaitļus, kas dalās ar \(7\). Cik ir tādu skaitļu, kas ir apvilkti ar vismaz divām dažādām krāsām?

LV.AMO.2016.7.5

Kvadrāts sadalīts \(12 \times 12\) vienādās kvadrātiskās rūtiņās un izkrāsots kā šaha galdiņš. Četrdesmit trijās baltajās rūtiņās sēž pa vienai mušai. Varde lēkā pa kvadrātu, katrā lēcienā šķērsojot divu rūtiņu kopējo malu. Tā nelec caur rūtiņu stūri un nelec rūtņā, kurā tā jau ir bijusi. Ielecot rūtiņā, kurā sēž muša, varde to apēd. Zināms, ka varde ir bijusi vismaz \(100\) rūtiņās. Pierādīt, ka varde ir apēdusi vismaz \(21\) mušu!

LV.AMO.2018.7.1

Cik dažādus naturālus skaitļus, kam visi cipari ir dažādi, var izveidot no cipariem \(2,\ 0,\ 1,\ 8\) ?

LV.AMO.2018.7.1

Cik dažādus naturālus skaitļus, kam visi cipari ir dažādi, var izveidot no cipariem \(2,\ 0,\ 1,\ 8\) ?

LV.AMO.2023.7.4

Latvijā, tāpat kā visās eirozonas valstīs, apgrozībā ir \(1\); \(2\); \(5\); \(10\); \(20\) un \(50\) centu monētas. Pieņemsim, ka ir zināma no šīm monētām izveidotā naudas summa \(S\) un izmantoto monētu skaits \(M\). Daudzos gadījumos, zinot \(S\) un \(M\) vērtības, var viennozīmīgi noteikt izmantoto monētu komplektu. Piemēram, ja \(S=7\) un \(M=3\), tad ir izmantota viena piecu un divas viena centa monētas un citu variantu nav.

Kāda ir mazākā \(S\) vērtība, kurai var atrast tādu \(M\) vērtību, ka, zinot \(S\) un \(M\) vērtības, izmantoto monētu komplektu viennozīmīgi nav iespējams noteikt?

LV.AMO.2024.7.2

Jurģis Mik̦eļdienas tirgū ar izlozes palīdzību izdalīja \(11\) balvas. Katra balva satur \(6\) rudens labumus: ābolus, bumbierus un bietes. Pie tam zināms, ka katra balva satur vismaz vienu ābolu, bumbieri un bieti. Pamatot, ka noteikti tika izdalītas divas tādas balvas, kurām bija vienāds saturs.

LV.AMO.2004.8.5

Virknē augošā kārtībā izrakstīti naturālie skaitļi no \(1\) līdz \(2004\) ieskaitot, katrs vienu reizi. Izsvītrojam no tās skaitļus, kas atrodas \(1.,\ 4.,\ 7.,\ 10.,\ \ldots\) vietās. No palikušās virknes atkal izsvītrojam skaitļus, kas tajā atrodas \(1.,\ 4.,\ 7.,\ \ldots\) vietās. Ar iegūto virkni rīkojamies tāpat, utt., kamēr paliek neizsvītrots viens skaitlis. Kurš tas ir?

LV.AMO.2022A.8.5

Mārtiņš augošā secībā pēc kārtas sāka rakstīt skaitļus, kuru pirmie četri cipari ir "\(3321\)":

\[3321; 33210; 33211; 33212; 33213; 33214;\ldots \]

Kāds ir \(3321.\) skaitlis šajā virknē?

LV.NOL.2013.8.3

Cik ir tādu četrciparu skaitļu, kuru pierakstā ir vismaz viens pāra cipars?

LV.NOL.2014.8.3

Cik ir tādu piecciparu skaitļu, kuru pierakstā ir vismaz viens nepāra cipars?

LV.AMO.2014.9.2

Doti četri dažādi cipari, neviens no tiem nav \(0\). Visu divciparu skaitļu, kurus var izveidot no šiem cipariem, summa ir \(1276\). Atrast dotos četrus ciparus!

LV.AMO.2019.9.1

Plaknē novilktas \(5\) vertikālas, \(4\) horizontālas un \(3\) savstarpēji paralēlas slīpas taisnes. Cik paralelogramu izveido šīs taisnes?

LV.AMO.2019.9.1

Plaknē novilktas \(5\) vertikālas, \(4\) horizontālas un \(3\) savstarpēji paralēlas slīpas taisnes. Cik paralelogramu izveido šīs taisnes?

LV.AMO.2019.9.1

Plaknē novilktas \(5\) vertikālas, \(4\) horizontālas un \(3\) savstarpēji paralēlas slīpas taisnes. Cik paralelogramu izveido šīs taisnes?

LV.AMO.2024.9.5

Ingai ir tālrunis ar šādu pogu izkārtojumu:

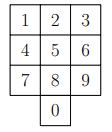
Viṇas draudzenes Zanes deviņciparu tālruņa numuram ir šādas īpašības:

visi Zanes tālruņa numura cipari ir atšk̦irīgi;
pirmie četri cipari ir sakārtoti augošā secībā un to attiecīgo pogu centri veido kvadrātu;
pēdējo četru ciparu pogu centri arı̄ veido kvadrātu;
Zanes tālruņa numurs dalās ar \(15\).

Cik ir tādu deviņciparu tālruņa numuru, kas varētu būt Zanes tālruņa numurs?

LV.AMO.2003.10.4

Rindā ir \(12\) krēslu; uz katra no tiem sēž pa skolēnam. Skolēniem vienu reizi atļauts piecelties un apsēsties citā kārtībā, pie tam katrs drīkst apsēsties vai nu iepriekšējā vietā, vai tieši blakus iepriekšējai vietai.

Cik dažādi skolēnu izvietojumi iespējami pēc pārkārtošanās?

LV.NOL.2010.10.4

Atrisināt naturālos skaitļos vienādojumu \(x^{3}=y!+2\).

LV.NOL.2013.10.4

Ansītis aprēķināja skaitļu \(2^{2013}\) un \(5^{2013}\) vērtības un iegūtos skaitļus uzrakstīja vienu aiz otra. Cik cipari uzrakstīti?

LV.NOL.2015.10.4

Vai eksistē tāds vesels skaitlis \(x\), ka visi skaitļi

(A) \(x,\ x+23,\ x+45,\ x+121\);
(B) \(x,\ x+23,\ x+46,\ x+121\)

ir veselu skaitļu pakāpes ar naturālu kāpinātāju, kas lielāks nekā \(1\) (kāpinātāji var būt dažādi)?

LV.NOL.2018.10.4

No cipariem \(1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9\), katru izmantojot divas reizes, izveidoti trīs sešciparu skaitļi. Ar kādu lielāko nuļļu skaitu var beigties trīs izveidoto skaitļu summa?

LV.VOL.2013.10.1

Pierādīt, ka vienādojumam \(\frac{1}{a}+\frac{1}{b}+\frac{1}{a^{2}+b^{2}}=\frac{1}{2}\) nav atrisinājuma naturālos skaitļos.

LV.AMO.2019.12.4

Sporta nometnē ir \(100\) skolēni. Ar \(N\) apzīmējam, cik veidos šos \(100\) skolēnus var sadalīt \(50\) pāros (pāru secība un arī skolēnu secība pārī nav svarīga). Ar kādu lielāko trijnieka pakāpi dalās \(N\)?