2.1.1.0.0. Kopu elementu skaitīšana ar vienkāršu aritmētiku
Reizināšanas, saskaitīšanas, atņemšanas un dalīšanas likumi.
- Reizināšanas likums kombinatorikā
- Saskaitīšanas likums kombinatorikā
- Dalīšanas likums kombinatorikā.
- Atņemšanas likums kombinatorikā.
LV.AMO.2016.7.5
Kvadrāts sadalīts \(12 \times 12\) vienādās kvadrātiskās rūtiņās un izkrāsots kā šaha galdiņš. Četrdesmit trijās baltajās rūtiņās sēž pa vienai mušai. Varde lēkā pa kvadrātu, katrā lēcienā šķērsojot divu rūtiņu kopējo malu. Tā nelec caur rūtiņu stūri un nelec rūtņā, kurā tā jau ir bijusi. Ielecot rūtiņā, kurā sēž muša, varde to apēd. Zināms, ka varde ir bijusi vismaz \(100\) rūtiņās. Pierādīt, ka varde ir apēdusi vismaz \(21\) mušu!
LV.AMO.2018.7.1
Cik dažādus naturālus skaitļus, kam visi cipari ir dažādi, var izveidot no cipariem \(2,\ 0,\ 1,\ 8\) ?
LV.AMO.2018.7.1
Cik dažādus naturālus skaitļus, kam visi cipari ir dažādi, var izveidot no cipariem \(2,\ 0,\ 1,\ 8\) ?
LV.AMO.2022A.8.5
Mārtiņš augošā secībā pēc kārtas sāka rakstīt skaitļus, kuru pirmie četri cipari ir "\(3321\)":
\[3321; 33210; 33211; 33212; 33213; 33214;\ldots \]
Kāds ir \(3321.\) skaitlis šajā virknē?LV.NOL.2013.8.3
Cik ir tādu četrciparu skaitļu, kuru pierakstā ir vismaz viens pāra cipars?
LV.NOL.2014.8.3
Cik ir tādu piecciparu skaitļu, kuru pierakstā ir vismaz viens nepāra cipars?
LV.AMO.2019.9.1
Plaknē novilktas \(5\) vertikālas, \(4\) horizontālas un \(3\) savstarpēji paralēlas slīpas taisnes. Cik paralelogramu izveido šīs taisnes?
LV.AMO.2019.9.1
Plaknē novilktas \(5\) vertikālas, \(4\) horizontālas un \(3\) savstarpēji paralēlas slīpas taisnes. Cik paralelogramu izveido šīs taisnes?
LV.AMO.2024.9.5
Ingai ir tālrunis ar šādu pogu izkārtojumu:
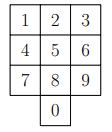
Viṇas draudzenes Zanes deviņciparu tālruņa numuram ir šādas īpašības:
- visi Zanes tālruņa numura cipari ir atšk̦irīgi;
- pirmie četri cipari ir sakārtoti augošā secībā un to attiecīgo pogu centri veido kvadrātu;
- pēdējo četru ciparu pogu centri arı̄ veido kvadrātu;
- Zanes tālruņa numurs dalās ar \(15\).
Cik ir tādu deviņciparu tālruņa numuru, kas varētu būt Zanes tālruņa numurs?
LV.AMO.2019.12.4
Sporta nometnē ir \(100\) skolēni. Ar \(N\) apzīmējam, cik veidos šos \(100\) skolēnus var sadalīt \(50\) pāros (pāru secība un arī skolēnu secība pārī nav svarīga). Ar kādu lielāko trijnieka pakāpi dalās \(N\)?