3.1.2.2.0. Trijstūra leņķu sakarības
Izmantot trijstūra iekšējo un ārējo leņķu sakarības
LV.AMO.2015.7.4
Vienādsānu trijstūrī \(ABC\) uz pamata malas \(BC\) atzīmēts iekšējs punkts \(D\) tā, ka arī trijstūri \(ABD\) un \(ACD\) ir vienādsānu. Aprēķini trijstūra \(ABC\) leņķus! Atrodi visus gadījumus un pamato, ka citu nav!
LV.AMO.2022B.8.3
In a triangle \(ABC\) on the side \(BC\) there is a point \(D\) such that \(AD = BD\) and \(AB = DC = AC\). Calculate the angles of \(ABC\)!
LV.AMO.2022B.8.3
Trijstūrī \(ABC\) uz malas \(BC\) atlikts tāds punkts \(D\), ka \(AD = BD\) un \(AB = DC = AC\). Aprēķināt trijstūra \(ABC\) leņķus!
LV.AMO.2023.8.3
Divi vienādmalu trijstūri novietoti plaknē kā parādīts 15. att. Zināms, ka \(\sphericalangle CAD = \alpha\) un \(\sphericalangle FDJ = \beta\). Izsaki leņķi \(CGF\) ar \(\alpha\) un \(\beta\).
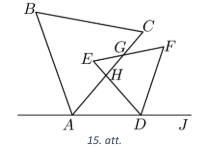
LV.AMO.2024.8.4
Uz riņk̦a līnijas ar centru \(O\) ir atlikti punkti \(A, B\) un \(C\) tā, lai punkts \(O\) atrastos trijstūrī \(ABC\). Pie tam zināms, ka \(\sphericalangle AOC=\alpha\), bet \(\sphericalangle OAB=\beta\). Izteikt leņķi \(\sphericalangle BCO\) ar \(\alpha\) un \(\beta\)!
LV.AMO.2017.9.3
Dots trijstūris \(ABC\), kuram \(AB>AC>BC\). Virsotnes \(A\) blakusleņķa bisektrise krusto malas \(BC\) pagarinājumu punktā \(D\), bet virsotnes \(C\) blakusleņķa bisektrise krusto malas \(AB\) pagarinājumu punktā \(E\). Zināms, ka \(AD=AC=CE\). Aprēķināt trijstūra \(ABC\) leņķus!
LV.AMO.2023.9.3
Trijstūrī viens leņķis ir par \(120^{\circ}\) lielāks nekā otrs. Pierādīt, ka bisektrise, kas vilkta no trešā leņķa virsotnes, ir divas reizes garāka nekā augstums no tās pašas virsotnes!