3.1.2.2.1. Trijstūra iekšējo leņķu summa
LV.AMO.2023.8.3
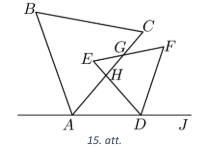
Divi vienādmalu trijstūri novietoti plaknē kā parādīts 15. att. Zināms, ka \(\sphericalangle CAD = \alpha\) un \(\sphericalangle FDJ = \beta\). Izsaki leņķi \(CGF\) ar \(\alpha\) un \(\beta\).
LV.AMO.2015.9.4
Vienādsānu trapeces \(ABCD\) sānu malas ir \(AB\) un \(CD\), bet diagonāles \(AC\) un \(BD\) krustojas punktā \(E\). Ap trijstūri \(CDE\) apvilktā riņķa līnija krusto garāko pamatu \(AD\) iekšējā punktā \(F\). Nogriežņu \(CF\) un \(BD\) krustpunkts ir \(G\). Nosaki \(\sphericalangle CGD\) lielumu, ja \(\sphericalangle CAD=\alpha\)!
LV.AMO.2017.9.3
Dots trijstūris \(ABC\), kuram \(AB>AC>BC\). Virsotnes \(A\) blakusleņķa bisektrise krusto malas \(BC\) pagarinājumu punktā \(D\), bet virsotnes \(C\) blakusleņķa bisektrise krusto malas \(AB\) pagarinājumu punktā \(E\). Zināms, ka \(AD=AC=CE\). Aprēķināt trijstūra \(ABC\) leņķus!
LV.AMO.2023.9.3
Trijstūrī viens leņķis ir par \(120^{\circ}\) lielāks nekā otrs. Pierādīt, ka bisektrise, kas vilkta no trešā leņķa virsotnes, ir divas reizes garāka nekā augstums no tās pašas virsotnes!