3.16.2.0.0. Dažādi uzdevumi rūtiņu lapā
Izmantot rūtiņu laukuma īpašības
LV.AMO.2012.5.5
Sadali 1.zīmējumā attēloto figūru trīs vienādās figūrās. (Figūru un tās spoguļattēlu saucam par vienādām figūrām.)
LV.AMO.2014.5.4
Kvadrāts sastāv no \(8 \times 8\) vienādām kvadrātiskām rūtiņām. Tas sagriezts daļās tā, ka griezumi iet pa rūtiņu robežām.
Kāds lielākais skaits daļu var būt tādas kā 2.zīm. attēlotā figūra (figūras var būt pagrieztas jebkurā stāvoklī)?
LV.AMO.2022B.5.2
Draw a hexagon with its sides on a square grid having perimeter equal to its area!
Note: The area is the number of little squares that make up the hexagon and the
perimeter is the number of sides of the little squares on its border.
LV.AMO.2022B.5.2
Pa rūtiņu līnijām uzzīmē tādu sešstūri, kuram perimetra un laukuma vērtības sakrīt!
Piezīme. Laukums ir sešstūri veidojošo rūtiņu skaits un perimetrs ir
rūtiņu malu, kas pilnībā atrodas uz robežas, skaits.
LV.AMO.2023.5.3
Rūtiņu lapā, kurā katras rūtiņas malas garums ir \(1\), uzzīmē daudzstūri, kuram gan perimetra, gan laukuma vērtība ir tāda pati kā malu skaits!
LV.AMO.2022B.6.2
Show how to cut ten shapes (as in Fig.2) from the given piece of grid paper (see Fig. 1). (Mark the lines where cuts should be made!) The figures can also be rotated.
LV.AMO.2022B.6.2
Parādi, kā no 1. att. dotās rūtiņu lapas var izgriezt desmit figūras,
kādas dotas 2. att. (iezīmē, kur jāiet griezuma līnijām)!
Figūras var būt arī pagrieztas.
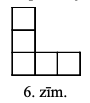
LV.AMO.2014.7.5
Kādu mazāko skaitu rūtiņu jāizgriež no kvadrāta \(6 \times 6\), lai no atlikušās daļas nevarētu izgriezt 6.zīm. parādīto figūru? (Figūru malām jāiet pa rūtiņu līnijām.)
LV.AMO.2018.7.5
Lauriņa no taisnstūra ar izmēriem \(7 \times 2018\) rūtiņas izgriež 5.att. dotās figūras, bet Pēcītis no tāda paša taisnstūra izgriež 6.att. dotās figūras. Kurš no viņiem var izgriezt vairāk figūru? Figūras var būt pagrieztas vai apgrieztas spoguļattēlā.
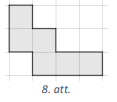
LV.AMO.2022A.7.3
Vai taisnstūri ar izmēriem \(3 \times 3370\) rūtiņas var noklāt ar 8.att. redzamām figūrām tā, lai paliktu tieši \(2022\) nenoklātas rūtiņas? Dotās figūras malām jāiet pa rūtiņu līnijām, tā var būt pagriezta vai apgriezta spoguļattēlā, figūras nedrīkst pārklāties vai iziet ārpus taisnstūra.
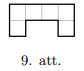
LV.AMO.2024.7.4
Dots kvadrāts ar izmēriem \(10 \times 10\) rūtiņas. Kāds ir lielākais skaits 9. att. redzamo figūru, kuras var izgriezt no šī kvadrāta, ja griezuma līnijām jāiet pa rūtiņu līnijām? Figūras drīkst būt pagrieztas.
LV.AMO.2018.8.5
(A) Kāds ir mazākais rūtiņu skaits, kas jāiekrāso \(6 \times 6\) rūtiņu
kvadrātā, lai katrā šī kvadrāta \(2 \times 3\) rūtiņu taisnstūrī (tas var būt arī
pagriezts vertikāli) būtu vismaz viena iekrāsota rūtiņa?
(B) Vai noteikti
tad, kad ir iekrāsots mazākais rūtiņu skaits, visas četras stūra rūtiņas paliks
neiekrāsotas?
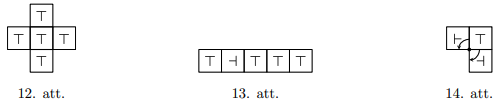
LV.AMO.2024.8.5
Dotas piecas smagas kastes un tās izkārtotas, kā tas redzams 12. att. Šīs kastes var pārvietot tikai pagriežot par 90 grādiem ap kādu no kastes stūriem. Kastes nav iespējams pārvietot citām kastēm virsū. Pēc vairākiem šādiem pārvietojumiem šīs kastes tika izkārtotas, kā tas redzams 13. att. Kuras no šīm kastēm varēja sākotnēji atrasties 12. att. izkārtojuma centrā? Piemēru, kā kasti var pārvietot ap vienu stūri divos dažādos veidos skatīt 14. att.
LV.AMO.2018.9.5
Kāds ir mazākais rūtiņu skaits, kas jāiekrāso taisnstūrī ar izmēriem \(5 \times 8\) rūtiņas, lai katrā šī taisnstūra \(2 \times 3\) rūtiņu taisnstūrī (tas var būt arī pagriezts vertikāli) būtu vismaz viena iekrāsota rūtiņa?
LV.AMO.2022A.9.5
Kāds mazākais skaits rūtiņu jāaizkrāso taisnstūrī ar izmēriem \(8 \times 8\) rūtiņas, lai nevarētu atrast nevienu taisnstūri ar izmēriem \(1 \times 5\) rūtiņas (kurš var būt novietots gan horizontāli, gan vertikāli), kuram visas rūtiņas ir neaizkrāsotas?