4.1.1.1.0. Dalāmības pazīmes ar 2 un 5 reizinājumiem
Dalāmības pazīmes, kurās pietiek aplūkot dažus pēdējos ciparus
LV.AMO.2022B.5.1
What is the smallest positive integer that uses only the digits \(0\) and \(2\) in its notation and is divisible by \(15\)?
LV.AMO.2022B.5.1
Kāds ir mazākais naturālais skaitlis, kura pierakstā izmantoti tikai cipari \(0\) un \(2\) un kurš dalās ar \(15\)?
LV.AMO.2005.7.4
Triju veselu pozitīvu skaitļu summa ir \(407\). Ar kādu lielāko daudzumu nuļļu var beigties šo skaitļu reizinājums?
LV.AMO.2008.7.2
Dots, ka \(x\) un \(y\) - tādi naturāli skaitļi, ka \(x \cdot y=10^{12}\). Vai var būt, ka ne \(x\), ne \(y\) nesatur savā pierakstā nevienu ciparu \(0\)?
LV.AMO.2013.7.3
Pierādīt, ka skaitlis \(1234567891011\ldots175176\) (pēc kārtas uzrakstīti visi naturālie skaitļi no \(1\) līdz \(176\)) nav naturāla skaitļa kvadrāts. (Skaitļa kvadrāts ir skaitļa reizinājums pašam ar sevi.)
LV.AMO.2019.7.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā septiņu naturālu skaitļu reizinājumu tā, lai to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2019.7.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā septiņu naturālu skaitļu reizinājumu tā, lai to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2022B.7.1
The following text was written on the board: \(A869B\). Each of the letters \(A\) and \(B\) must be replaced by one digit (they may or may not be the same) so that the resulting five-digit number is divisible by \(15\). In how many ways can you do this?
LV.AMO.2022B.7.1
Uz tāfeles bija uzrakstīts šāds teksts: \(A869B\). Katrs no burtiem \(A\) un \(B\) jāaizstāj ar vienu ciparu (tie var būt arī vienādi) tā, lai iegūtais piecciparu skaitlis dalītos ar \(15\). Cik dažādos veidos to var izdarīt?
LV.AMO.2023.7.2
Kāds ir lielākais iespējamais septiņciparu skaitlis, kuram vienlaicīgi izpildās šādi nosacījumi:
- tas dalās ar \(12\);
- skaitļa pirmais cipars ir tāds pats kā pēdējais cipars;
- skaitļa 2., 4. un 6. cipars ir vienādi un tie ir divas reizes lielāki nekā pirmais cipars;
- skaitļa trešais cipars ir tāds pats kā piektais cipars?
LV.AMO.2006.8.3
Naturāla skaitļa \(x\) ciparu summu apzīmēsim ar \(S(x)\). Pieņemsim, ka \(n\) - tāds naturāls skaitlis, kam vienlaicīgi izpildās īpašības \(S(n)=10\) un \(S(5n)=5\).
(A) atrodiet kaut vienu tādu skaitli,
(B) vai tādu skaitļu ir bezgalīgi daudz?
(C) vai kāds no tādiem skaitļiem ir nepāra?
LV.AMO.2016.8.3
Zināms, ka skaitlis dalās ar \(2016\) un ka visi tā cipari ir dažādi. Kāds ir lielākais ciparu skaits, kas var būt šajā skaitlī?
LV.AMO.2019.8.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā sešu naturālu skaitļu reizinājumu tā, ka neviens no tiem nav mazāks kā \(10\) un to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2019.8.5
Kādai mazākajai naturālai \(n\) vērtībai skaitli \(10^{n}\) iespējams izteikt kā sešu naturālu skaitļu reizinājumu tā, ka neviens no tiem nav mazāks kā \(10\) un to visu pēdējie cipari ir dažādi (tas ir, nevienam no tiem pēdējais cipars nesakrīt ar kāda cita skaitļa pēdējo ciparu)?
LV.AMO.2022B.8.1
The following text was written on the board: \(N597M\). Each of the letters \(N\) and \(M\) should be replaced by a digit (they may or may not be the same) so that the resulting five digit number is divisible by \(12\). In how many ways can you do this?
LV.AMO.2022B.8.1
Uz tāfeles bija uzrakstīts šāds teksts: \(N597M\). Katrs no burtiem \(N\) un \(M\) jāaizstāj ar vienu ciparu (tie var būt arī vienādi) tā, lai iegūtais piecciparu skaitlis dalītos ar \(12\). Cik dažādos veidos to var izdarīt?
LV.NOL.2016.8.2
Karlīna uzrakstīja divus skaitļus, kuru pierakstā nav izmantots cipars \(0\). Katru ciparu viņa aizstāja ar burtu: dažādus ciparus - ar dažādiem burtiem, vienādus - ar vienādiem. Viens no uzrakstītajiem skaitļiem \(DUBĻUNNN\) dalās ar \(104\). Pierādi, ka otrais skaitlis \(BURBUĻUVANNA\) nedalās ar \(56\).
LV.AMO.2024.9.5
Ingai ir tālrunis ar šādu pogu izkārtojumu:
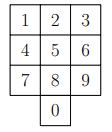
Viṇas draudzenes Zanes deviņciparu tālruņa numuram ir šādas īpašības:
- visi Zanes tālruņa numura cipari ir atšk̦irīgi;
- pirmie četri cipari ir sakārtoti augošā secībā un to attiecīgo pogu centri veido kvadrātu;
- pēdējo četru ciparu pogu centri arı̄ veido kvadrātu;
- Zanes tālruņa numurs dalās ar \(15\).
Cik ir tādu deviņciparu tālruņa numuru, kas varētu būt Zanes tālruņa numurs?
LV.NOL.2017.10.5
Desmitciparu skaitlī vienādus ciparus aizvietojot ar vienādiem burtiem, bet dažādus- ar dažādiem, ieguva vārdu MATEMĀTIKA (īsais " \(A\) " un garais " \(Ā\) " aizstāj atšķirīgus ciparus). Papildus zināms, ka skaitlis \(\overline{MA}\) dalās ar \(2\), \(\overline{MAT}\)- ar \(3\), \(\overline{MATE}\)- ar \(4\), \(\overline{\text { MATEM }}\)- ar \(5\), \(\overline{MATEM \bar{A}}\)- ar \(6\), \(\overline{MATEM \bar{A}T}\)- ar \(7\), \(\overline{MATEM \bar{A}TI}\)- ar \(8\), \(\overline{MATEM \bar{A}TIK}\)- ar \(9\), \(\overline{MATEM \bar{A}TIKA}\)- ar \(10\). Noteikt, kāds bija sākotnējais desmitciparu skaitlis!
LV.NOL.2017.10.5
Desmitciparu skaitlī vienādus ciparus aizvietojot ar vienādiem burtiem, bet dažādus- ar dažādiem, ieguva vārdu MATEMĀTIKA (īsais " \(A\) " un garais " \(Ā\) " aizstāj atšķirīgus ciparus). Papildus zināms, ka skaitlis \(\overline{MA}\) dalās ar \(2\), \(\overline{MAT}\)- ar \(3\), \(\overline{MATE}\)- ar \(4\), \(\overline{\text { MATEM }}\)- ar \(5\), \(\overline{MATEM \bar{A}}\)- ar \(6\), \(\overline{MATEM \bar{A}T}\)- ar \(7\), \(\overline{MATEM \bar{A}TI}\)- ar \(8\), \(\overline{MATEM \bar{A}TIK}\)- ar \(9\), \(\overline{MATEM \bar{A}TIKA}\)- ar \(10\). Noteikt, kāds bija sākotnējais desmitciparu skaitlis!
LV.NOL.2019.10.5
Atrast visus pirmskaitļu pārus \((m, n)\), kuriem \(20m+18n=2018\).
LV.VOL.2017.10.2
Dots pirmskaitlis, kas satur vismaz \(4\) dažādus ciparus. Pierādīt, ka tā ciparus var pārkārtot citā secībā tā, lai jauniegūtais skaitlis nebūtu pirmskaitlis!
LV.VOL.2018.10.3
Skaitļus \(a,\ b,\ c\) sauksim par skaistu trijnieku, ja tiem piemīt šādas īpašības:
- tie ir trīs pēc kārtas esoši naturāli skaitļi;
- katrs no tiem dalās ar savu ciparu summu.
Piemēram, skaists trijnieks ir \(8,\ 9,\ 10\).
(A) Atrast tādu skaistu trijnieku, kurā mazākais skaitlis ir lielāks nekā \(10\).
(B) Pierādīt, ka eksistē bezgalīgi daudz skaistu trijnieku!