1.2.0.0.0. Vienādojumi
Algebras uzdevumi, kuros prasīts atrisināt vienādojumu vai noteikt vienādojuma sakņu skaitu. Uzdevumi, kuros jāpēta vienādojuma atrisinājuma eksistence, jāpierāda, ka eksistē atrisinājums vai ka tas neeksistē.
LV.AMO.2014.5.1
Pūkainīšu ciemata bērniem Lieldienu zaķis atnesa olas. Katra no tām bija nokrāsota tieši vienā no krāsām- sarkanā, dzeltenā, zilā. Zināms, ka \(20 \%\) jeb \(40\) olas bija sarkanas, \(\frac{3}{4}\) no atlikušajām bija dzeltenas, bet pārējās- zilas. Aprēķini:
(A) Cik olas bija zilā krāsā?
(B) Kāda daļa no visām olām bija zilas?
(C) Cik procenti no visām olām bija dzeltenas?
LV.AMO.2014.7.4
Tabulas \(3 \times 3\) rūtiņās katrā rūtiņā jāieraksta pa vienam naturālam skaitlim tā, lai katrā rindā, katrā kolonnā un katrā diagonālē ierakstīto skaitļu summas būtu vienādas. Ir zināmi divās rūtiņās ierakstītie skaitļi (skat. 5.zīm.). Kādam skaitlim jābūt rūtiņā, kas apzīmēta ar jautājuma zīmi? Atrodiet visas iespējamās vērtības un pamatojiet, ka citu nav!
LV.AMO.2022A.7.1
Attālināto mācību laikā skolēni iemācījās ļoti ātri atbildēt uz testa jautājumiem. Vilnis uz \(4\) jautājumiem var atbildēt \(30\) sekundēs, bet Raimonds uz pieciem jautājumiem var atbildēt \(40\) sekundēs. Skolotāja bija sagatavojusi testu ar ļoti daudz jautājumiem. Vilnim bija nepieciešama \(1\) stunda, lai atbildētu uz visiem šī testa jautājumiem. Cik ilgā laikā šo pašu testu izpildīja Raimonds?
LV.AMO.2022B.7.2
Do there exist (A) \(5\); (B) \(15\) positive integers (some of them may be equal) such that their sum equals their product?
LV.AMO.2022B.7.2
Vai var atrast (A) \(5\); (B) \(15\) naturālus skaitļus (ne obligāti dažādus), kuru summa ir vienāda ar to reizinājumu?
LV.AMO.2024.7.1
Marta, Sandris un Linda vēlas sagatavot pulciņa telpu Ziemassvētku ballītei. Zināms, ka Marta viena pati to spētu izdarīt vienā stundā, Sandris to spētu pusotrā stundā, bet Linda to spētu izdarīt trīs stundās. Marta ieradās pulciņa telpā 16:00, Sandris \(10\) minūtēs vēlāk, bet Linda vēl 15 minūtes pēc Sandra (katrs pēc ierašanās uzreiz k̦ērās pie pulciņa telpas gatavošanas). Cikos pulciņa telpa bija gatava?
LV.AMO.2003.8.1
Vienādojumiem \(x^{2}+p_{1}x+q_{1}=0\), \(x^{2}+p_{2}x+q_{2}=0\) un \(x^{2}+p_{3}x+q_{3}=0\) ir attiecīgi saknes \(x_{0}\) un \(x_{1}\), \(x_{0}\) un \(x_{2}\), \(x_{0}\) un \(x_{3}\). Izteikt vienādojuma \(x^{2}+\frac{p_{1}+p_{2}+p_{3}}{3} x+\frac{q_{1}+q_{2}+q_{3}}{3}=0\) saknes ar \(x_{0},\ x_{1},\ x_{2}\) un \(x_{3}\), nelietojot kvadrātsaknes zīmi.
LV.AMO.2014.8.2
Atrast visus naturālos skaitļus, kas nepārsniedz \(1000000\) un kuri, nosvītrojot to pirmo ciparu, samazinās \(15\) reizes!
LV.AMO.2014.8.5
Tabulas \(3 \times 3\) rūtiņās katrā rūtiņā jāieraksta pa vienam naturālam skaitlim tā, lai katrā rindā, katrā kolonnā un katrā diagonālē ierakstīto skaitļu summas būtu vienādas. Augšējās rindas vidējā rūtiņā ierakstīts skaitlis \(24\) (skat. 9.zīm.). Vai rūtiņā, kas apzīmēta ar jautājuma zīmi, var būt ierakstīts skaitlis (A) \(7\), (B) \(17\)?
LV.AMO.2019.8.1
Atjaunojot taisnu žogu, Raimonds izraka vecos žoga stabus, kuri atradās \(8\) metru attālumā viens no otra un kuru skaits bija nepāra skaitlis. Raimonds sanesa visus stabus pie vidējā, nesdams tos pa vienam un sākdams ar vienu no malējiem stabiem. Cik bija stabu, ja viņš nostaigāja \(840~\mathrm{m}\)?
LV.AMO.2014.9.2
Doti četri dažādi cipari, neviens no tiem nav \(0\). Visu divciparu skaitļu, kurus var izveidot no šiem cipariem, summa ir \(1276\). Atrast dotos četrus ciparus!
LV.AMO.2014.9.4
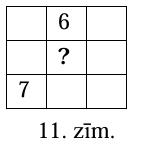
Tabulas \(3 \times 3\) rūtiņās katrā rūtiņā jāieraksta pa vienam naturālam skaitlim tā, lai katrā rindā, katrā kolonnā un katrā diagonālē ierakstīto skaitļu summas būtu vienādas, bet visi tabulā ierakstītie skaitļi ir savā starpā atšķirīgi. Ir zināmi divās rūtiņās ierakstītie skaitļi (skat. 11.zīm.). Kāds ir mazākais skaitlis, kas var būt ierakstīts tabulas centrālajā rūtiņā?
LV.AMO.2015.9.3
Pierādi, ka \(x^{5}-5x^{3}+4x\) dalās ar \(120\), ja \(x\) ir vesels skaitlis!
LV.AMO.2017.9.5
Atrisināt naturālos skaitļos vienādojumu \(x^{3}+(x+1)^{3}=(x+3)^{3}+1\).
LV.AMO.2018.9.1
Dots vienādojums \((a-3)x^{2}+5x-2=0\).
(A) Kādām \(a\) vērtībām vienādojumam ir
tieši viena sakne?
(B) Kādām \(a\) vērtībām vienādojumam ir divas dažādas
reālas saknes?
LV.AMO.2019.9.5
Vai eksistē tāds kvadrātvienādojums ar veseliem koeficientiem, kuram ir sakne
\[(\sqrt{2020}-2 \sqrt{2019}+\sqrt{2018})(\sqrt{2020}+\sqrt{2019})(\sqrt{2019}+\sqrt{2018})(\sqrt{2020}+\sqrt{2018})?\]
LV.AMO.2024.9.1
Doti reāli skaitļi \(a\) un \(b\), kuriem
\[\frac{a}{a^{2}-5}=\frac{b}{5-b^{2}}=\frac{a b}{a^{2} b^{2}-5}.\]
Kāda var būt izteiksmes \(a^{4}+b^{4}\) vērtība, ja papildus zināms, ka \(a+b \neq 0\)?