LV.VOL.2013.10.5 lv
Dota rūtiņu lapa ar izmēriem \(n \times m\) (\(n, m\)- naturāli skaitļi) rūtiņas. Divi spēlētāji spēlē šādu spēli, pēc kārtas izdarot pa vienam gājienam. Ar vienu gājienu atļauts veikt taisnu griezienu, kas sākas kādā lapas malā un iet pa rūtiņu malām, pie tam griezuma garumam jābūt naturālam skaitlim. Zaudē tas spēlētājs, pēc kura gājiena lapa tiek sagriezta divos atsevišķos gabalos. Kādām \(n\) un \(m\) vērtībām, pareizi spēlējot, vienmēr var uzvarēt pirmais spēlētājs, un kad - otrais (spēli vienmēr sāk pirmais spēlētājs)?
Atrisinājums
Šķirosim divus gadījumus:
- Skaitļi \(n\) un \(m\) abi ir nepāra. Šajā gadījumā \(2.\) spēlētājs vienmēr var veikt griezumu, kas ir simetrisks \(1.\) spēlētāja pēdējam griezumam attiecībā pret lapas centru (skat., piem., 6.zīm.). Tāpēc šajā gadījumā uzvar \(2.\) spēlētājs.
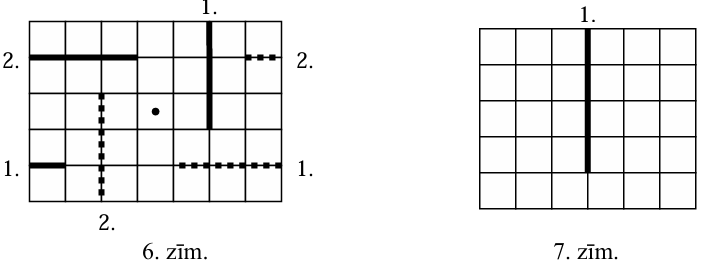
- Vismaz viens no skaitļiem \(n\) un \(m\) ir pāra. Tad \(1.\) spēlētājs sākumā veic visgarāko iespējamo griezumu pa vidu malā ar pāra garumu (skat. 7.zīm.). Tālāk \(1.\) spēlētājs var pielietot (1) punkta \(2.\) spēlētāja simetrisko stratēģiju. Tāpēc šajā gadījumā uzvar \(1.\) spēlētājs.