Atrisinājums

(A) Tā kā \(n\) ir pāra skaitlis, tad \(n=2 k, k \in \mathbb{N}\), un kopā tabulā ir \(n^{2}=(2 k)^{2}=4 k^{2}\) rūtiņu. Tādā gadījumā tabulu var sadalīt ar \(k^{2}\) kvadrātos, kuru izmēri ir \(2 \times 2\) rūtiṇas. Lai katra šāda kvadrāta skaitlu reizinājums dalītos ar \(5\), tad kādā no rūtiṇām ir jāatrodas skaitla \(5\) daudzkārtnim. Tātad kopā nepieciešami \(k^{2}\) atškirīgi skaitļi, kas dalās ar \(5\), tas ir, \(5;10;15;\ldots;5k^{2}\). Lielākais tabulā ierakstītais skaitlis ir \(4 k^{2}<5 k^{2}\), tāpēc nepietiek skaitla \(5\) daudzkārtṇu, ko ierakstīt katrā no kvadrātiem ar izmēriem \(2 \times 2\). Līdz ar to tabula nav sakarīga.

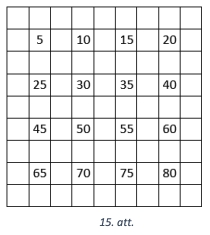
(B) Pamatosim, ka lielākā \(n\) vērtība ir \(9\). Ja \(n=2 k+1\) ir nepāra skaitlis, tad tabulu, neieskaitot pēdējo rindu un pēdējo kolonnu, var sadalīt \(k^{2}\) kvadrātos, kuru izmēri ir \(2 \times 2\) rūtiṇas. Tādā gadījumā nepieciešami vismaz \(k^{2}\) skaitḷa \(5\) daudzkārtṇi, lai iegūtu sakarīgu tabulu. Pavisam tabulā ierakstīti \(n^{2}=(2 k+1)^{2}=4 k^{2}+4 k+1\) skaitḷi, tāpēc nepieciešams, lai \(4 k^{2}+4 k+1 \geq 5 k^{2}\) (lai pietiktu skaitlaa \(5\) daudzkārtṇu). Līdz ar to iegūstam nevienādību \(k^{2} \leq 4 k+1\), kas ir patiesa naturāliem skaitlliem \(k \leq 4\), tāpēc lielākā \(k\) vērtība ir \(4\) un attiecīgi lielākā \(n\) vērtība ir \(9\). Skaitļus kvadrātā ar izmēriem \(9 \times 9\) rūtinas var sarakstīt, piemēram, kā redzams 15. att., kurā atlikušos skaitļus var ierakstīt patvaļīgi.