LV.NOL.2023.8.3 en lv
Dots vienādsānu trijstūris \(ABC\), kuram \(AB = BC\). Uz malas \(AB\) izvēlēts punkts \(M\) un uz malas \(BC\) izvēlēts punkts \(K\) tā, ka \(AM = AK = AC\). Zināms, ka \(AK \perp MC\). Aprēḳināt trijstūra \(ABC\) leņkus!
Atrisinājums
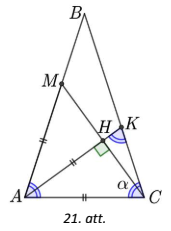
Apzīmējam \(AK\) un \(MC\) krustpunktu ar \(H\) (skat. 21.att.). Tā kā \(\triangle KAC\) un \(\triangle ABC\) ir vienādsānu trijstūri, tad \(\sphericalangle AKC=\sphericalangle ACK=\sphericalangle BAC=\alpha\). Nogrieznis \(AH\) ir vienādsānu trijstūra \(MAC\) augstums pret pamatu, tātad arī bisektrise, tāpēc \(\sphericalangle KAC=\sphericalangle BAC: 2=\frac{\alpha}{2}\). Tā kā trijstūra \(KAC\) iekšējo leņku summa ir \(180^{\circ}\), tad iegūstam, ka \(\frac{\alpha}{2}+\alpha+\alpha=180^{\circ}\), no kurienes \(\frac{5}{2} \alpha=180^{\circ}\) jeb \(\alpha=72^{\circ}\).
Tātad \(\sphericalangle BAC = \sphericalangle ACB = 72^{\circ}\) un \(\sphericalangle B=180^{\circ} - 2 \cdot 72^{\circ}=36^{\circ}\).