LV.NOL.2023.11.2 en lv
Kādā zemē dzīvo rūķi, katri divi no tiem vai nu draudzējas, vai viens otru ienīst. Zināms, ka nav tādu trīs rūḳu, kas visi viens otru ienīst. Vai noteikti var atrast tādus trīs rūḳus, kas visi savā starpā draudzējas, ja šajā zemē ir (A) \(5\) rūķi, (B) \(6\) rūķi?
Atrisinājums
Katru rūķi apzīmēsim ar punktu. Ja divi rūḳi draudzējas, tad tos savienosim ar zaḷu nogriezni (nepārtraukta līnija), ja tie viens otru ienīst, tad savienosim tos ar sarkanu nogriezni (pārtraukta līnija).
(A) Nē, var gadīties, ka nav tādu trīs rūḳu, kas visi savā starpā draudzējas, piemēram, skat. 7. att.
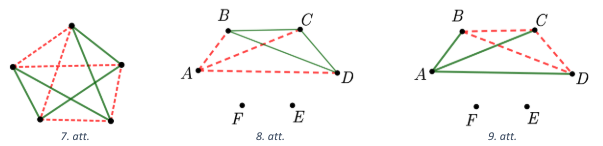
(B) Pamatosim, ka noteikti var atrast tādus trīs rūķus, kas visi savā starpā draudzējas.
Apskatām punktu \(A\). No tā iziet vismaz \(3\) vienas krāsas nogriežņi, jo katri divi rūķi vai nu draudzējas, vai ir ienaidnieki un no viena punkta iziet \(5\) nogriežņi (pēc Dirihlē principa). Apskatām abus iespējamos gadījumus, kādā krāsā var būt nogriežņi \(AB\), \(AC\) un \(AD\).
- Ja nogriežņi \(AB\), \(AC\), \(AD\) ir sarkanā krāsā (ienīst), tad nogriežņiem \(B C, C D, B D\) ir jābūt zaḷā krāsā (skat. 8.att.), lai neveidotos sarkani trijstūri \(ABC\), \(ACD\) un \(ABD\), jo pēc dotā nav tādu trīs rūķu, kas visi ienīst viens otru. Tātad ir trīs rūki \(B,C\) un \(D\), kas visi draudzējas savā starpā (veidojas zals̆ trijstūris \(BCD\)).
- Nogriežņi \(AB\), \(AC\), \(AD\) ir zalạ krāsā (draudzējas). Pieņemsim pretējo, ka nav tādu trīs rūķu, kas visi savā starpā draudzējas (nav zaḷa trijstūra). Tad punkti \(B,C,D\) jāsavieno ar sarkaniem nogriežņiem \(BC\), \(CD\), \(BD\) (skat. 9.att.), lai neviens no trijstūriem \(ABC\), \(ACD\) un \(ABD\) nebūtu zaļš. Bet tādā gadījumā rūķi \(B,C,D\) visi viens otru ienīst, kas ir pretrunā ar doto. Tātad pieņēmums ir aplams un ir tādi trīs rūķi, kas visi savā starpā draudzējas.