LV.NOL.2015.11.5 lv
Dots taisnstūris ar izmēriem \(n \times m\) rūtiņas. Sākumā katrā rūtiņā ir ierakstīts \(5\). Māris dotajā taisnstūrī veic secīgas darbības:
- izvēlas kādu taisnstūri un visās tā rūtiņās ieraksta ciparu \(1\);
- izvēlas kādu taisnstūri un visās tā rūtiņās ieraksta ciparu \(2\);
- izvēlas kādu taisnstūri un visās tā rūtiņās ieraksta ciparu \(3\);
- visbeidzot izvēlas kādu taisnstūri un visās tā rūtiņās ieraksta ciparu \(4\).
Katra izvēlētā taisnstūra malām jāiet pa rūtiņu līnijām un cipars vienmēr jāraksta rūtiņā jau esošā skaitļa labajā pusē.
Vai iespējams, ka visās rūtiņās ierakstītie skaitļi ir dažādi, ja dotā taisnstūra izmēri ir (A) \(3 \times 6\), (B) \(3 \times 5\), (C) \(4 \times 4\) rūtiņas?
Atrisinājums
Rūtiņās var būt ierakstīti \(16\) atšķirīgi skaitļi:
\[\begin{gathered} 5 \\ 51;\ 52;\ 53;\ 54; \\ 512;\ 513;\ 514;\ 523;\ 524;\ 534; \\ 5123;\ 5124;\ 5134;\ 5234; \\ 51234. \end{gathered}\]
**(A)** Tā kā taisnstūrī \(3 \times 6\) ir \(18\) rūtiņas, tad pēc Dirihlē principa vismaz divās rūtiņās ierakstītie skaitļi būs vienādi. Tātad nav iespējams, ka visās laukuma rūtiņās ierakstītie skaitļi atšķiras. **(B)** Tā kā taisnstūrī \(3 \times 5\) ir \(15\) rūtiņas, tad tieši viens skaitlis nebūs ierakstīts. Ievērojam, ka katrs no cipariem \(1,\ 2,\ 3\) un \(4\) parādās astoņos skaitļos. Tātad katrs no cipariem \(1,\ 2,\ 3,\ 4\) būs ierakstīts \(7\) vai \(8\) rūtiņās. Tā kā katrs cipars ir ierakstīts taisnstūrveida laukumā, tad vienīgais iespējamais taisnstūra izmērs ir \(2 \times 4\) rūtiņas (pretējā gadījumā pēc Dirihlē principa vismaz divās rūtiņās ierakstītie skaitļi būs vienādi). Vēl varam ievērot, ka jebkuru divu ciparu pāris ir sastopams tieši četros skaitļos. Līdz ar to katriem diviem taisnstūriem drīkst būt kopīgas ne vairāk kā četras rūtiņas. Taisnstūrī ar izmēriem \(3 \times 5\) rūtiņas taisnstūri \(2 \times 4\) rūtiņas var novietot četros dažādos veidos (skat. A7.zīm.).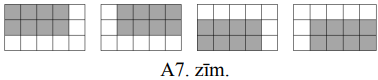
Taisnstūriem, kas atrodas pie augšējās malas, pārklājas sešas rūtiņas - tātad vairākās no tām ierakstīto skaitļu komplekti būs vienādi un panākt, ka visās rūtiņās ierakstītie skaitļi ir atšķirirīgi, nav iespējams.
(C) Jā, ir iespējams, ka visās laukuma rūtiņās ierakstītie skaitļi atšķiras (skat., piemēram, A8.zīm.).
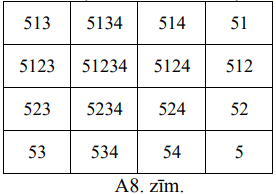
Taisnstūrus var izvēlēties, piemēram, kā parādīts A9.zīm.