LV.NOL.2013.12.4 lv
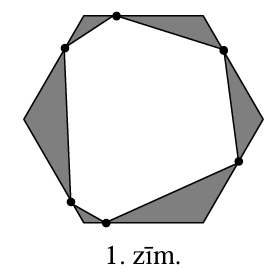
Dots regulārs sešstūris ar malas garumu \(1\). Uz katras malas ir patvaļīgi izvēlēts viens punkts (skat. 1.zīm.). Pierādīt, ka vismaz viena iekrāsotā trijstūra laukums nepārsniedz \(\frac{\sqrt{3}}{16}\).
Atrisinājums
Sauksim par doto \(6\) trijstūru sānu malām tās malas, kas atrodas uz sešstūra malām. Aplūkosim šo trijstūru abu sānu malu garumu summas. Tā kā dotā sešstūra perimetrs ir vienāds ar \(6\), no Dirihlē principa seko, ka vismaz viena šāda summa nav lielāka kā \(1\) (jo visas trijstūru sānu malas pilnībā nosedz visas sešstūra malas). Apzīmēsim šo trijstūri ar \(\Delta\) un tā sānu malas ar \(a\) un \(b\), tad \(a+b \leq 1\). No nevienādības starp vidējo aritmētisko un vidējo ģeometrisko seko:
\[\begin{align*} & 2 \sqrt{ab} \leq a+b \leq 1 \\ & ab \leq\left(\frac{a+b}{2}\right)^{2} \leq\left(\frac{1}{2}\right)^{2} \\ & ab \leq \frac{1}{4} \tag{1} \end{align*}\]
Trijstūra \(\Delta\) laukumu varam aprēķināt pēc formulas \(\frac{1}{2} ab \sin \alpha\), kur \(\alpha\) ir leņķis starp malām \(a\) un \(b\). Tā kā dots regulārs sešstūris, tad \(\alpha=120^{\circ}\). Tāpēc trijstūra \(\Delta\) laukums ir vienāds ar\[\begin{equation*} \frac{1}{2} ab \sin \alpha=\frac{1}{2} ab \sin 120^{\circ}=\frac{1}{2} ab \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4} ab \tag{2} \end{equation*}\]
No (1) un (2) seko, ka trijstūra \(\Delta\) laukums nav lielāks kā \(\frac{\sqrt{3}}{4} \cdot \frac{1}{4}=\frac{\sqrt{3}}{16}\), k.b.j.