Atrisinājums

(A) Mēģināsim panākt pretējo, tas ir, iekrāsot rūtiņas dotajā kvadrātā tā, lai nav taisnstūra ar izmēriem \(2 \times 4\) rūtiņas bez iekrāsotām rūtiņām.

Visu laukumu sadalām kvadrātos ar izmēriem \(2 \times 2\) rūtiņas, kurus nosauksim par šūnām (skat. 24. att., kur katrā šūnā norādīts tās numurs).

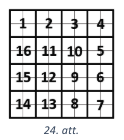
Tā kā katrā rindā un katrā kolonnā ir iekrāsota tieši viena rūtiņa, tad katrā šūnā var būt iekrāsotas 0, 1 vai 2 rūtiņas. Ja kādā šūnā būs atzīmētas divas rūtiņas, tad attiecīgajā šūnu rindā un šūnu kolonnā pārējās šūnas būs bez iekrāsotām rūtiņām, turklāt vismaz divās blakus šūnās nebūs iekrāsotu rūtiņu, šīs šūnas kopā veidos \(2 \times 4\) rūtiņu taisnstūri bez iekrāsotām rūtiņām (pretruna ar pieņēmumu). Tātad katrā šūnā drīkst iekrāsot ne vairāk kā 1 rūtiņu. Tā kā kopā ir iekrāsotas tieši \(8\) rūtiņas, tad astoņās no \(16\) šūnām jābūt iekrāsotai tieši vienai rūtiņai.

Pamatosim: ja divas šūnas ar iekrāsotu rūtiņu atradīsies blakus, tad kaut kur blakus atradīsies divas šūnas bez iekrāsotām rūtiņām. Ievērojam, ka doto kvadrātu var pagriezt tā, lai šīs divas blakus šūnas ar iekrāsotajām rūtiņām būtu ar secīgiem numuriem (mazākais numurs ir nepāra) kā parādīts 24. att.

Tad atlikušās šūnas secīgi var sadalīt pa pāriem, iegūstot \(7\) šūnu pārus. Lai nebūtu taisnstūris bez iekrāsotām rūtiņām, tad vismaz katrā otrajā šūnā jāiekrāso rūtiņa. Tas nozīmē, ka nepieciešams pa rūtiņai atzīmēt vismaz \(7\) šūnās, kas nav iespējams, jo atlikušais iekrāsojamo rūtiņu skaits ir \(6\). Tātad šūnām ar iekrāsotajām rūtiņām jābūt izvietotām šaha galdiņa veidā (skat. 25. att.).

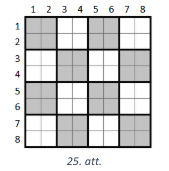
Simetrijas dēļ varam pieņemt, ka 1. šūna satur iekrāsotu rūtiņu. Aplūkosim 11. šūnu un pieņemsim, ka tajā iekrāsotā rūtiņa atrodas šūnas kreisajā pusē (tas ir, sākotnējā kvadrāta 3. kolonnā). Vai nu 3. šūnā, vai 9. šūnā iekrāsotajai rūtiņai ir jāatrodas 6. kolonnā (jo kolonnā drīkst būt iekrāsota tikai viena rūtiņa), tad taisnstūris ar izmēriem \(2 \times 4\) bez iekrāsotām rūtiņām parādīts attiecīgi 26. att. un 27. att.

Gadījums, kad 11. šūnā iekrāsotā rūtiņa atrodas šūnas labajā pusē, ir simetrisks, tad taisnstūris ar izmēriem \(2 \times 4\) bez iekrāsotām rūtiņām parādīts 28. att. un 29. att.

Līdz ar to jebkurā kvadrātā ar doto iekrāsojumu var atrast taisnstūri ar izmēriem \(2 \times 4\) rūtiņas, kurā nav iekrāsota neviena rūtiņa.

(B) Piemēram, skat. 30. att., kurā nevar atrast \(2 \times 5\) taisnstūri ar neatzīmētu rūtiņu.