LV.AMO.2023.10.3 lv
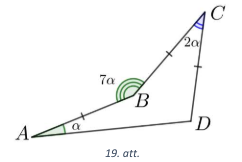
Dots ieliekts četrstūris \(ABCD\), kuram \(AB=BC=CD\). Zināms, ka \(\sphericalangle BAD = \alpha\) un \(\sphericalangle BCD = 2\alpha\), bet leņķa \(ABC\) lielums četrstūra ārpusē ir \(7\alpha\) (skat. 19. att.). Aprēķināt \(\alpha\) vērtību!
Atrisinājums
Vispirms atliekam punktus \(B'\) un \(C'\), kas ir attiecīgi punktu \(B\) un \(C\) simetriskie punkti attiecībā pret taisni \(AD\) (skat. 21. att.).
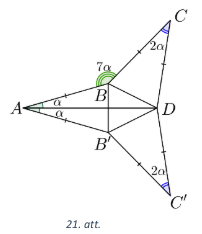
Savienojam punktus \(B\) un \(D\), kā arī \(B'\) un \(D\). Rezultātā izveidosies trīs vienādsānu trijstūri: \(\triangle ABB'\), \(\triangle B'C'D\) un \(\triangle CBD\). Šie trijstūri ir savā starpā vienādi pēc pazīmes \(m\ell{}m\), jo to virsotnes leņķi \(\sphericalangle B'AB = \sphericalangle BCD = \sphericalangle DC'B'\) un sānu malu garumi ir savstarpēji vienādi. Tātad \(\triangle BB'D\) ir vienādmalu trijstūris un \(\sphericalangle B'BD = 60^{\circ}\). Tā kā \(\triangle ABB'\) ir vienādsānu, tad tā pamata leņķis \(\sphericalangle ABB'=90^{\circ} - \alpha\). Līdzīgi varam spriest par \(\triangle CBD\) pamata leņķi \(\sphericalangle CBD = 90^{\circ} - \alpha\).
Tagad aplūkojam četrstūra \(ABCD\) iekšējo leņķi \(\sphericalangle ABC\). Izmantojot doto, iegūstam, ka tā lielums ir \(\sphericalangle ABC = 360^{\circ} − 7\alpha\). No otras puses, tas ir vienāds ar
\[\sphericalangle ABB' + \sphericalangle B'BD + \sphericalangle CBD = 90^{\circ} - \alpha + 60^{\circ} + 90^{\circ} - \alpha = 240^{\circ} - 2\alpha\]
Tātad\[360^{\circ} − 7\alpha = 240^{\circ} − 2\alpha \;\;\Rightarrow\;\; \alpha = 24^{\circ}.\]