LV.AMO.2022B.11.3 en lv
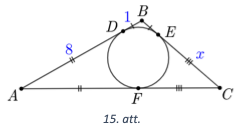
Trijstūrī \(ABC\) ievilktā riņķa līnija pieskaras malai \(AB\) punktā \(D\) tā, ka \(AD = 8\) un \(BD = 1\). Aprēķināt malas \(BC\) garumu, ja trijstūra leņķa \(B\) lielums ir \(120^{\circ}\).
Atrisinājums
Apzīmējam riņka līnijas pieskaršanās punktu malai \(BC\) ar \(E\) un malai \(AC\) ar \(F\) skat. 15.att. Tā kā trijstūrī \(ABC\) ir ievilkta riņķa līnija, tad pieskaru nogriežņi ir vienādi: \(BD=BE=1\), \(AD=AF=8\) un \(CE=CF=x\). Tātad \(AB=9, BC=1+x, AC=8+x\). Izmantojot kosinusu teorēmu, iegūstam
\(AC^{2} = AB^{2} + BC^{2} - 2 \cdot AB \cdot BC \cdot \cos \sphericalangle B\)
\((8+x)^{2}=9^{2}+(1+x)^{2}-2 \cdot 9 \cdot(1+x) \cdot \cos 120^{\circ}\)
\(64+16 x+x^{2}=81+1+2 x+x^{2}-2 \cdot 9(1+x) \cdot(-0,5)\)
\(5x=27\)
\(x=5.4\).
Tātad \(BC=1+x=6.4\).