LV.AMO.2022B.10.3 en lv
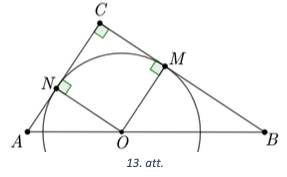
Uz taisnleņķa trijstūra \(ACB\) hipotenūzas \(AB\) atlikts punkts \(O\), kas ir centrs riņķa līnijai ar rādiusu \(3\), kura pieskaras abām katetēm. Aprēķināt trijstūra \(ACB\) laukumu, ja \(OB = 5\).
Atrisinājums
Punktus, kur riņķa līnijas rādiuss pieskaras katetēm, apzīmēsim ar \(M\) un \(N\) (skat. 13. att.). Tā kā rādiuss ir perpendikulārs pieskarei, tad trijstūris \(OMB\) ir taisnleņka trijstūris. Pēc Pitagora teorēmas \(MB=\sqrt{OB^{2}-MO^{2}}=\sqrt{25-9}=4 \mathrm{~cm}\).
Tā kā rādiusi ir perpendikulāri pieskarēm un trijstūris \(ACB\) ir taisnleņka, tad četrstūra ONCM trīs leņki ir taisni \(\sphericalangle NCM=\sphericalangle CNO=\sphericalangle CMO=90^{\circ}\). Četrstūra \(ONCM\) divas blakusmalas ir vienādas \(ON=OM\) kā rādiusi, tāpēc četrstūris \(ONCM\) ir kvadrāts un \(MC=OM=3 \mathrm{~cm}\), \(CB=BM+MC=7 \mathrm{~cm}\). Ievērojam, ka \(\triangle OMB \sim \triangle ACB\) pēc pazīmes \(\ell \ell\), jo \(\sphericalangle B\) ir kopīgs un \(\sphericalangle OMB=\sphericalangle ACB=90^{\circ}\). Tad \(\frac{AC}{OM}=\frac{CB}{MB'}\), no kā iegūstam, ka \(AC=\frac{OM \cdot CB}{MB}=\frac{3 \cdot 7}{4}=5,25 \mathrm{~cm}\). Līdz ar to \(S_{ACB}=\frac{AC \cdot CB}{2}=18 \frac{3}{8} \mathrm{~cm}^{2}\).