Atrisinājums

Regulārā sešstūra virsotnes apzīmējam ar \(A, B, C, D, E, F\).

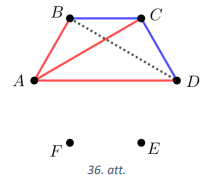
(A) Pierādīsim, ka vienmēr būs vismaz viens vienkrāsas trijstūris. Pieņemsim, ka nav neviena vienkrāsas trijstūra. Aplūkojam patvaļīgu sešstūra virsotni \(A\). Tā kā no tās iziet \(5\) nogriežņi, tad vismaz trīs no tiem ir vienā krāsā (Dirihlē princips). Nezaudējot vispārīgumu, uzskatīsim, ka nogriežņi \(\textcolor{red}{AB}, \textcolor{red}{AC}, \textcolor{red}{AD}\) ir sarkanā krasā. Tad \(\textcolor{blue}{BC}\) un \(\textcolor{blue}{CD}\) jābūt zilā krāsā un viens no trijstūriem \(ABD\) vai \(BCD\) ir vienkrāsas trijstūris (skat. 36.att.). Iegūta pretruna ar pieņēmumu.

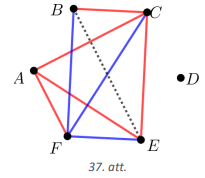
(B) Nē, nevar. Pierādīsim, ka vienmēr būs vismaz divi vienkrāsas trijstūri. Pieņemsim, ka ir tikai viens vienkrāsas trijstūris. Nezaudējot vispārīgumu, varam uzskatīt, ka tas ir sarkans trijstūris \(\textcolor{red}{ACE}\) (skat. 37.att.). Vismaz viena no trijstūra \(FBD\) malām \(FB,\ BD\) vai \(DF\) ir zilā krāsā, pretējā gadījumā uzreiz būtu divi vienkrāsas trijstūri. Nezaudējot vispārīgumu, varam uzskatīt, ka \(FB\) ir zila. Viens no nogriežņiem \(AF\) vai \(AB\) ir sarkans, jo pretējā gadījumā būtu divi vienkrāsas trijstūri. Simetrijas dēļ varam uzskatīt, ka \(\textcolor{red}{AF}\) ir sarkans. Tad \(\textcolor{blue}{FE}\) un \(\textcolor{blue}{FC}\) ir zilā krāsā, bet \(\textcolor{red}{BC}\) ir sarkanā krāsā. Tagad vai nu \(FEB\), vai \(BEC\) ir vienkrāsas trijstūris. Iegūta pretruna ar pieņēmumu.