3.3.3.3.0. Vienādsānu trijstūri
Izmantot vienādsānu trijstūru īpašības
LV.AMO.2003.7.4
Izliektā piecstūrī \(ABCDE\) punkti \(A_{1},\ B_{1},\ C_{1},\ D_{1},\ E_{1}\) ir attiecīgi malu \(CD,\ DE,\ EA,\ AB,\ BC\) viduspunkti. Dots, ka \(AA_{1} \perp CD,\ BB_{1} \perp DE,\ CC_{1} \perp EA\) un \(DD_{1} \perp AB\). Pierādiet, ka \(EE_{1} \perp BC\).
LV.AMO.2016.7.3
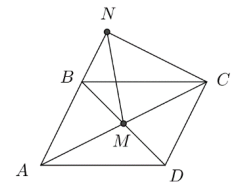
Dots, ka \(AB \| CD\) un \(AD \| BC\) (skat. 9.att.). Nogriežņu \(AC\) un \(BD\) krustpunkts ir \(M\). Uz taisnes \(AB\) izvēlēts tāds punkts \(N\), ka \(AM=MN\). Pierādīt, ka \(\sphericalangle ANC=90^{\circ}\).
LV.AMO.2017.7.3
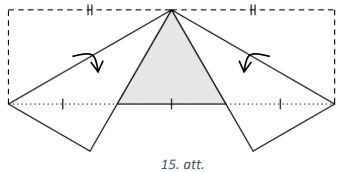
Divus taisnstūra lapas stūrus nolocīja tā, kā parādīts 15.att. Izrādījās, ka lapas apakšējā mala tika sadalīta trīs vienāda garuma nogriežņos un augšējā mala - divos vienāda garuma nogriežņos. Pierādīt, ka iekrāsotais trijstūris ir vienādmalu!
LV.AMO.2019.7.3
Izliektā četrstūrī \(ABCD\) leņķu \(BAD\) un \(ADC\) bisektrises krustojas punktā \(M\). Pierādīt, ka \(BM=CM\), ja zināms, ka \(AD=AB+CD\).
Piezīme. Četrstūri sauc par izliektu, ja visi tā iekšējie leņķi ir mazāki nekā \(180^{\circ}\).
LV.AMO.2015.8.5
Šaurleņķu trijstūrī \(ABC\) novilkts augstums \(CH\) un mediāna \(BK\). Zināms, ka \(CH=BK\) un \(\sphericalangle HCB=\sphericalangle KBC\). Pierādīt, ka trijstūris \(ABC\) ir vienādmalu!
LV.AMO.2019.8.3
Dots paralelograms \(ABCD\). Leņķa \(BAD\) bisektrise krusto malu \(BC\) iekšējā punktā \(E\) un \(CD\) pagarinājumu punktā \(F\). Pierādīt, ka \(BC=DF\), ja zināms, ka \(DE\) ir perpendikulārs \(AF\).
LV.AMO.2022A.8.3
Kvadrātā \(ABCD\) novilkta diagonāle \(AC\) un uz tās atzīmēts punkts \(E\) tā, ka \(\sphericalangle DEC=75^{\circ}\). Nogriežņa \(DE\) pagarinājums krusto malu \(AB\) punktā \(F\). Pierādīt, ka \(EF=FB\)!
LV.AMO.2022B.8.3
In a triangle \(ABC\) on the side \(BC\) there is a point \(D\) such that \(AD = BD\) and \(AB = DC = AC\). Calculate the angles of \(ABC\)!
LV.AMO.2022B.8.3
Trijstūrī \(ABC\) uz malas \(BC\) atlikts tāds punkts \(D\), ka \(AD = BD\) un \(AB = DC = AC\). Aprēķināt trijstūra \(ABC\) leņķus!
LV.AMO.2024.8.4
Uz riņk̦a līnijas ar centru \(O\) ir atlikti punkti \(A, B\) un \(C\) tā, lai punkts \(O\) atrastos trijstūrī \(ABC\). Pie tam zināms, ka \(\sphericalangle AOC=\alpha\), bet \(\sphericalangle OAB=\beta\). Izteikt leņķi \(\sphericalangle BCO\) ar \(\alpha\) un \(\beta\)!
LV.AMO.2017.9.3
Dots trijstūris \(ABC\), kuram \(AB>AC>BC\). Virsotnes \(A\) blakusleņķa bisektrise krusto malas \(BC\) pagarinājumu punktā \(D\), bet virsotnes \(C\) blakusleņķa bisektrise krusto malas \(AB\) pagarinājumu punktā \(E\). Zināms, ka \(AD=AC=CE\). Aprēķināt trijstūra \(ABC\) leņķus!
LV.AMO.2022B.9.3
In a right triangle \(ACB\) (\(\sphericalangle C = 90^{\circ}\)) \(CH\) is an altitude. On the side \(AC\) we mark a point \(K\) so that \(\sphericalangle CBK = \sphericalangle BAC\). Prove that the line \(CH\) divides the segment \(BK\) in half!
LV.AMO.2022B.9.3
Taisnleņķa trijstūrī \(ACB\) (\(\sphericalangle C = 90^{\circ}\)) novilkts augstums \(CH\). Uz malas \(AC\) atlikts punkts \(K\) tā, ka \(\sphericalangle CBK = \sphericalangle BAC\). Pierādīt, ka taisne \(CH\) dala nogriezni \(BK\) divās vienādās daļās!