2.2.3.1.4. Pilna sakārtojuma attiecības
Binārā attiecība \(R\) ir pilna sakārtojuma attiecība, ja tā ir refleksīva, pilna (ir spēkā vai nu \(aRb\) vai \(b\)), antisimetriska (no \(aRb\) un \(bRa\) loģiski seko \(a=b\)) un transitīva. Pilna sakārtojuma attiecība skaitļu kopā ir, piemēram, \(\leq\) ("mazāks vai vienāds" jeb "nepārsniedz").
LV.AMO.2017.9.4
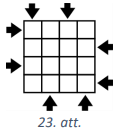
(A) Pierādi, ka dotajā \(4 \times 4\) rūtiņu laukumā (skat. 23.att.) nevar ierakstīt \(16\) dažādus naturālus skaitļus tā, lai katrā rūtiņā būtu ierakstīts viens skaitlis un katrā rindā un katrā kolonnā skaitļi pieaugtu bultiņas norādītajā virzienā.
(B) Kāds mazākais bultiņu skaits jāapvērš pretējā virzienā, lai skaitļus varētu izvietot saskaņā ar uzdevuma nosacījumiem?
LV.AMO.2018.9.4
Atrast lielāko naturālo skaitli, kas dalās ar \(7\), kura ciparu summa ir \(100\) un kuram neviens cipars nav \(0\).