3.1.1.4.0. Iekšējie un ārējie šķērsleņķi
LV.AMO.2016.7.3
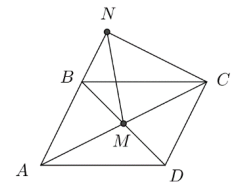
Dots, ka \(AB \| CD\) un \(AD \| BC\) (skat. 9.att.). Nogriežņu \(AC\) un \(BD\) krustpunkts ir \(M\). Uz taisnes \(AB\) izvēlēts tāds punkts \(N\), ka \(AM=MN\). Pierādīt, ka \(\sphericalangle ANC=90^{\circ}\).
LV.AMO.2017.7.3
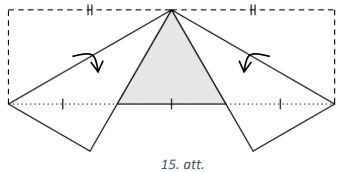
Divus taisnstūra lapas stūrus nolocīja tā, kā parādīts 15.att. Izrādījās, ka lapas apakšējā mala tika sadalīta trīs vienāda garuma nogriežņos un augšējā mala - divos vienāda garuma nogriežņos. Pierādīt, ka iekrāsotais trijstūris ir vienādmalu!
LV.AMO.2019.8.3
Dots paralelograms \(ABCD\). Leņķa \(BAD\) bisektrise krusto malu \(BC\) iekšējā punktā \(E\) un \(CD\) pagarinājumu punktā \(F\). Pierādīt, ka \(BC=DF\), ja zināms, ka \(DE\) ir perpendikulārs \(AF\).
LV.AMO.2019.9.3
Dots vienādsānu taisnleņķa trijstūris \(ABC\) ar taisno leņķi \(C\). Uz tā hipotenūzas konstruēts taisnstūris \(ABNM\) tā, ka punkti \(C\) un \(N\) atrodas dažādās pusēs no taisnes \(AB\) un \(AC=AM\). Nogrieznis \(CM\) krusto \(AB\) punktā \(P\). Punkts \(L\) ir malas \(MN\) viduspunkts. Nogrieznis \(CL\) krusto \(PN\) punktā \(Q\). Pierādīt, ka (A) trijstūris \(CBP\) ir vienādsānu; (B) četrstūris \(QNBC\) ir rombs!