2.3.1.0.0. Spēles ar simetriju
Simetrijas izmantošana spēļu analīzē. Spēles ar tiešu simetriju. Spēles ar vispārinātu simetriju.
LV.AMO.2003.7.3
Divi spēlētāji pamīšus raksta uz tāfeles pa vienam naturālam skaitlim no \(1\) līdz \(9\) ieskaitot. Nedrīkst rakstīt skaitļus, ar kuriem dalās kaut viens jau uzrakstīts skaitlis. Kas nevar izdarīt gājienu, zaudē.
Parādiet, kā tas, kas izdara pirmo gājienu, var uzvarēt.
LV.AMO.2019.7.2
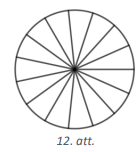
Riņķis sadalīts \(15\) vienādās daļās (skat. 12.att.). Divi spēlētāji pamīšus tās aizkrāso. Vienā gājienā drīkst aizkrāsot vai nu vienu no šīm daļām, vai divas blakus esošas daļas. Spēlētājs, kurš nevar izdarīt gājienu, zaudē. Kurš spēlētājs - pirmais vai otrais - vienmēr var uzvarēt?
LV.AMO.2019.8.2
Divi spēlētāji pamīšus izvieto kauliņus tabulas \(6 \times 6\) rūtiņās. Vienā gājienā var aizpildīt vai nu vienu tukšu rūtiņu, vai vairākas tukšas rūtiņas, kuras atrodas vai nu vienā rindā, vai vienā kolonnā. Tas spēlētājs, kas nevar izdarīt gājienu, zaudē. Kurš spēlētājs - pirmais vai otrais - vienmēr var uzvarēt?
LV.AMO.2019.9.2
Divi spēlētāji pamīšus aizkrāso tabulas \(9 \times 9\) rūtiņas. Spēlētājs, kurš spēli sāk, krāso rūtiņas melnā krāsā, viņa pretinieks - zilā krāsā. Vienā gājienā drīkst aizkrāsot tieši vienu rūtiņu. Kad visas rūtiņas ir aizkrāsotas, tad saskaita, cik ir tādu rindu un kolonnu, kuros melno rūtiņu ir vairāk nekā zilo - tie ir punkti, kurus ieguvis pirmais spēlētājs. Rindu un kolonnu skaits, kuros zilo rūtiņu ir vairāk nekā melno, ir otrā spēlētāja iegūtie punkti. Uzvar tas spēlētājs, kurš ir ieguvis vairāk punktu. Kurš spēlētājs - pirmais vai otrais - vienmēr var uzvarēt?