2.3.5.0.0. Spēles invariants
Spēles, kurās uzvarošo stratēģiju var pamatot, izmantojot invariantu (kādu īpašību, kuru spēlētājs ar uzvarošo stratēģiju vienmēr var atjaunot).
LV.AMO.2022B.7.4
There's a pile of candies on the table. Karlsson and Lillebror
take turns making moves, with Karlsson starting the game.
In one move, a player can remove from the pile and
eat either one or two candies. The player who eats the last candy wins.
Which player, can always win if there are initially
(A) \(6\) candies in the heap; (B) \(2022\) candies in the heap?
(Note: Karlsson and Lillebror are characters from A.Lindgren's
book Karlsson-on-the-Roof.)
LV.AMO.2022B.7.4
Uz galda ir kaudze ar konfektēm. Karlsons un Brālītis pēc kārtas izdara gājienus, Karlsons sāk spēli. Vienā gājienā spēlētājs var paņemt no kaudzes un apēst vai nu vienu, vai divas konfektes. Uzvar tas spēlētājs, kurš apēd pēdējo konfekti. Kurš spēlētājs, pareizi spēlējot, vienmēr var uzvarēt, ja sākumā kaudzē ir (A) \(6\) konfektes; (B) \(2022\) konfektes?
LV.AMO.2011.8.5
Jānis un Anna spēlē šādu spēli. Uz tāfeles ir uzrakstīts naturāls skaitlis. Spēlētāji pēc kārtas veic gājienu: no uzrakstītā skaitļa atnem kādu šī skaitļa ciparu (izņemot \(0\)), nodzēš uz tāfeles esošo skaitli un tā vietā uzraksta iegūto starpību. Uzvar tas, kurš pēc sava gājiena iegūst nulli.
Sākumā ir uzrakstīts skaitlis \(2011\), pirmo gājienu izdara Anna. Kurš no spēlētājiem, pareizi spēlējot, uzvarēs? Apraksti, kā uzvarētājam jārīkojas!
LV.AMO.2016.8.5
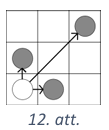
Divi spēlētāji spēlē spēli uz \(N \times N\) rūtiņas liela laukuma. Sākumā laukuma kreisajā apakšējā rūtiņā atrodas spēļu kauliņš. Katrā gājienā spēļu kauliņu drīkst pārvietot vai nu vienu lauciņu pa labi, vai vienu lauciņu uz augšu, vai arī divus lauciņus pa diagonāli uz augšu pa labi (skat. 12.att., kur kauliņa sākumpozīcija apzīmēta ar baltu, bet atļautie gājieni -- ar pelēkiem aplīšiem). Kauliņu nedrīkst pārvietot ārpus laukuma robežām. Spēlētāji gājienus izdara pēc kārtas. Zaudē spēlētājs, kurš nevar izdarīt gājienu. Kurš no spēlētājiem, pareizi spēlējot, uzvar, ja (A) \(N=7\), (B) \(N=8\)?
LV.AMO.2003.9.5
Uz galda atrodas \(k\) konfektes. Andris un Juris pamīšus izdara gājienus: Andris - pirmo, trešo, piekto, \(\ldots\), Juris - otro, ceturto, sesto, \(\ldots\) . Ar \(n\)-to gājienu \((n=1,\ 2,\ 3,\ \ldots)\) jāapēd vismaz viena, bet ne vairāk par \(n\) konfektēm. Kas apēd pēdējo konfekti, uzvar.
Kurš uzvar, pareizi spēlējot, ja (A) \(k=8\), (B) \(k=64\)?
LV.AMO.2019.11.2
Divi spēlētāji pamīšus raksta uz tāfeles skaitļa \(216\) naturālos dalītājus. Katrā gājienā jāievēro šādi noteikumi:
- nedrīkst atkārtoti rakstīt jau uzrakstītu dalītāju;
- nedrīkst rakstīt dalītāju, kurš ir tieši \(2\) vai \(3\) reizes lielāks vai mazāks nekā kāds jau uzrakstītais dalītājs.
Zaudē tas spēlētājs, kurš nevar izdarīt gājienu. Kurš spēlētājs - pirmais vai otrais - vienmēr var uzvarēt?