1.5.4.3.0. Cita saskaitāmo vai reizinātāju pārgrupēšana
LV.AMO.2017.8.2
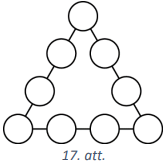
Vai katrā tukšajā aplītī (skat. 17.att.) var ierakstīt vienu naturālu skaitli tā, lai aplīšos būtu ierakstīti visi naturālie skaitļi no \(1\) līdz \(9\) un lai skaitļu summa uz katras trijstūra malas būtu (A) \(22\); (B) \(23\)?
LV.AMO.2018.8.4
Par maģisko kvadrātu sauc \(n \times n\) rūtiņu tabulu, kuras rūtiņās ierakstīti skaitļi no \(1\) līdz \(n^{2}\) tā, ka visās tabulas rindās, kolonnās un uz abām galvenajām diagonālēm rūtiņās ierakstīto skaitļu summas ir vienādas. (Katrs no skaitļiem ierakstīts tieši vienā rūtiņā.) Vai noteikti maģiskā kvadrāta centrālajā rūtiņā ir ierakstīts skaitlis \(\frac{n^{2}+1}{2}\), ja (A) \(n=3\), (B) \(n=5\)?