1.5.4.1.0. Saskaitīšana divos veidos
Metode, kas pierāda izteiksmju vienādību, pamatojot, ka to var saskaitīt divos veidos.
LV.AMO.2022B.6.5
Some of \(273\) villagers always tell the truth, the remaining ones lie all the time. Each of the villagers has exactly one favourite day of the week. There was a poll of all the villagers, and they were asked to answer seven questions with either "Yes" or "No":
| Question | ||
|---|---|---|
| Is Monday your favorite day? | \(\square\) Yes | \(\square\) No |
| Is Tuesday your favorite day? | \(\square\) Yes | \(\square\) No |
| Is Wednesday your favorite day? | \(\square\) Yes | \(\square\) No |
| Is Thursday your favorite day? | \(\square\) Yes | \(\square\) No |
| Is Friday your favorite day? | \(\square\) Yes | \(\square\) No |
| Is Saturday your favorite day? | \(\square\) Yes | \(\square\) No |
| Is Sunday your favorite day? | \(\square\) Yes | \(\square\) No |
The number of "Yes" answers received to each question was as follows: Monday - \(51\), Tuesday - \(52\), Wednesday - \(53\), Thursday - \(55\), Friday - \(54\), Saturday - \(56\), Sunday - \(57\). How many villagers lie all the time?
LV.AMO.2022B.6.5
Daži no 273 ciema iedzīvotājiem visu laiku saka patiesību,
pārējie visu laiku melo. Katram no ciema iedzīvotājiem
ir tieši viena mīļākā nedēļas diena. Aptaujājot iedzīvotājus,
viņiem tika lūgts atbildēt uz septiņiem jautājumiem,
katrā no tiem izvēloties vienu no dotajām atbildēm:

Uz katru jautājumu saņemto apstiprinošo ("jā") atbilžu skaits bija šāds:
pirmdiena – \(51\), otrdiena – \(52\),
trešdiena – \(53\), ceturtdiena – \(54\), piektdiena – \(55\),
sestdiena – \(56\), svētdiena – \(57\). Cik ciema iedzīvotāji visu laiku melo?
LV.AMO.2017.7.2
Katrā tukšajā lodziņā (skat. 12.att.) ieraksti vienu naturālu skaitli tā, lai figūrā būtu ierakstīti visi naturālie skaitļi no \(1\) līdz \(19\) un lai skaitļu summa visās joslās būtu viena un tā pati!
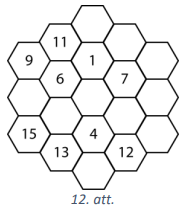
Piezīme. Visas iespējamās joslas skat. 13.att., tās var būt pagrieztas.

LV.AMO.2022B.7.5
Some of \(272\) villagers always tell the truth, the remaining ones lie all the time. Each of the villagers has exactly one favourite day of the week. There was a poll of all the villagers, and they were asked to answer seven questions with either "Yes" or "No":

The number of "Yes" answers received to each question was as follows: Monday - \(53\), Tuesday - \(54\), Wednesday - \(55\), Thursday - \(57\), Friday - \(56\), Saturday - \(58\), Sunday - \(59\). How many villagers lie all the time?
LV.AMO.2022B.7.5
Daži no \(272\) ciema iedzīvotājiem visu laiku saka patiesību, pārējie visu laiku melo. Katram no ciema iedzīvotājiem ir tieši viena mīļākā nedēļas diena. Aptaujājot iedzīvotājus, viņiem tika lūgts atbildēt uz septiņiem jautājumiem, katrā no tiem izvēloties vienu no dotajām atbildēm:

Uz katru jautājumu saņemto apstiprinošo ("jā") atbilžu skaits bija šāds: pirmdiena – \(53\), otrdiena – \(54\), trešdiena – \(55\), ceturtdiena – \(56\), piektdiena – \(57\), sestdiena – \(58\), svētdiena – \(59\). Cik ciema iedzīvotāju visu laiku melo?
LV.AMO.2024.7.5
Anita, Maija, Ināra un Sandra uzstājās koncertā. Katru dziesmu dziedāja 3 meitenes. Cik dziesmu meitenes nodziedāja pavisam, ja Anita dziedāja 7 dziesmas (vairāk nekā jebkura cita meitene), bet Sandra dziedāja 4 dziesmas (mazāk nekā jebkura cita meitene)?
LV.AMO.2018.8.4
Par maģisko kvadrātu sauc \(n \times n\) rūtiņu tabulu, kuras rūtiņās ierakstīti skaitļi no \(1\) līdz \(n^{2}\) tā, ka visās tabulas rindās, kolonnās un uz abām galvenajām diagonālēm rūtiņās ierakstīto skaitļu summas ir vienādas. (Katrs no skaitļiem ierakstīts tieši vienā rūtiņā.) Vai noteikti maģiskā kvadrāta centrālajā rūtiņā ir ierakstīts skaitlis \(\frac{n^{2}+1}{2}\), ja (A) \(n=3\), (B) \(n=5\)?
LV.AMO.2024.8.2
Pa apli patvaļīgā secībā sarakstīti visi naturālie skaitḷi no \(1\) līdz \(10\). Pamatot, ka noteikti var atrast tādus trīs secīgus skaitļus, kuru summa būs vismaz \(17\).
LV.AMO.2003.9.2
Kvadrāts sastāv no \(4 \times 4\) rūtiņām. Vai var tajās ierakstīt naturālus skaitļus no \(1\) līdz \(16\) (katrā rūtiņā - citu skaitli) tā, lai skaitļu summas visās rindās un kolonnās būtu dažādas un visas dalītos ar (A) \(4\), (B) \(8\)?
LV.AMO.2014.9.5
Katram marsietim ir trīs rokas un dažas antenas. Visi marsieši sadevās rokās (katrs marsietis sadevās rokās ar \(3\) citiem marsiešiem tā, ka visas rokas bija aizņemtas). Izrādījās, ka katriem diviem marsiešiem, kas bija sadevuši rokās, antenu skaits atšķīrās tieši \(6\) reizes. Vai kopējais antenu skaits visiem marsiešiem var būt \(2014\)?
LV.AMO.2023.9.4
Uz katras no \(36\) kartītēm uzrakstīts kāds naturāls skaitlis (daži no tiem var būt arī vienādi). Kartītes iespējams sadalīt deviņās grupās pa četrām kartītēm katrā tā, ka visās grupās uz kartītēm uzrakstīto skaitļu summas ir vienādas. Kā arī kartītes iespējams sadalīt četrās grupās pa deviņām kartītēm katrā tā, ka visās grupās uz kartītēm uzrakstīto skaitļu summas ir vienādas. Vai vienmēr visas kartītes var sadalīt sešās grupās pa sešām kartītēm katrā tā, ka visās grupās uz kartītēm uzrakstīto skaitļu summas ir vienādas?