LV.VOL.2025.10.4
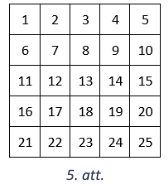
Dots \(5 \times 5\) rūtiṇu kvadrāts, kurā katrā rūtiṇā ierakstīts skaitlis no \(1\) līdz \(25\) (skat. 5.att.). No šī kvadrāta izgrieza \(6\) figūras, kas katra bija vai nu \(1 \times 4\) rūtiņu taisnstūris (vertikāls vai horizontāls), vai arī \(2 \times 2\) rūtiṇu kvadrāts, pāri palika viena rūtiņa. Kāds skaitlis var būt rakstīts uz šīs rūtiņas?
Atrisinājums
Parādīsim, ka pāri palikusī rūtiṇa ir stūra rūtiṇa, t.i., uz tās ir rakstīts \(1\), \(5\), \(21\) vai \(25\). Tas, ka tā var būt stūra rūtiṇa, redzams šajā piemērā (skat. 6. att.), lai iegūtu pārējās stūra rūtiṇas, attēls jāpagriež. Atliek pamatot, ka citu iespēju nav.
Vispirms ievērosim, ka katrā izgrieztajā figūrā ir divi pāra un nepāra skaitļi. Tātad atlikusī viena rūtiṇa noteikti satur nepāra skaitli (jo to mums ir vairāk). Aplūkosim rūtiṇas, uz kurām rakstīts \(8\), \(12\), \(14\) un 18 (kas visi ir pāra skaitļi, tātad šīs rūtiṇas noteikti tika izgrieztas). Ievērosim, ka
- šīs rūtiṇas pieder vismaz trim dažādām figūrām, kas izriet no tā, ka jebkura figūra, kas satur divas no šīm rūtiṇām, satur arī centrālo rūtiņu \(13\),
- neviena figūra, kas satur kādu no šīm rūtiṇām, nevar saturēt nevienu stūra rūtiṇu.
Tas nozīmē, ka uz visām četrām stūra rūtiņām mums ir atlikušas tikai trīs figūras, kam tās var piederēt. Tā kā divas stūra rūtiṇas nevar atrasties vienā figūrā, tad viena no tām paliks neizgriezta.
Atrisinājums
Parādīsim, ka pāri palikusī rūtiņa ir stūra rūtiņa, t.i., uz tās ir rakstīts \(1,5,21\) vai 25. Tas, ka tā var būt stūra rūtiņa, redzams šajā piemērā (skat. 6. att.), lai iegūtu pārējās stūra rūtiṇas, attēls jāpagriež. Atliek pamatot, ka citu iespēju nav. Lai pamatotu atrisinājuma otro daḷu, (ka nevar būt izgriezta neviena cita rūtiṇa, izṇemot stūra rūtiṇu) var izmantot arī šādu alternatīvu spriedumu: Ierakstīsim skaitḷus rūtinās tā, kā parādīts 7. att.
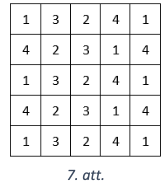
Ievērosim, ka jebkura pieḷaujamā \(1 \times 4\) vai \(2 \times 2\) figūra satur skaitļus, kuru summa ir \(10\). Tā kā visu skaitļu summa ir \(61\), tad skaidrs, ka vienīgā pāri palikusī rūtiṇa satur skaitli \(1\). Ja tā būtu kāda cita rūtiṇa, kas satur \(1\), izṇemot stūra rūtiņu, tad pagriežot visu "griezumu" par \(90\) grādiem vienu vai atspogulojot pret vertikālo simetrijas asi, mēs vienmēr varēsim panākt, ka pāri palikusī rūtiṇa satur kādu citu skaitli, kas nav \(1\) (kas nav iespējams). Tātad vienīgā iespēja ir, ka neizgriezta ir palikusi stūra rūtiņa.