LV.VOL.2023.11.3 lv
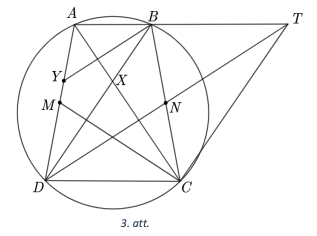
Dota vienādsānu trapece \(ABCD\), tās pamati ir \(AB\) un \(CD\) un diagonāles krustojas punktā \(X\). Malas \(AD\) viduspunktu apzīmēsim ar \(M\). Caur \(X\) vilktā taisne, kas paralēla \(AB\), krusto malu \(AD\) punktā \(Y\). Pierādīt, ka punkti \(B,C,M,Y\) atrodas uz vienas riṇka līnijas!
Atrisinājums
Lai pierādītu, ka ap četrstūri \(BCMY\) var apvilkt riņķa līniju, pietiek pierādīt, ka \(\sphericalangle M Y B+\sphericalangle M C B=180^{\circ}\) jeb \(\sphericalangle M C B=180^{\circ}-\sphericalangle M Y B\). Tā kā \(\sphericalangle M Y B=180^{\circ}-\sphericalangle A Y B\) (blakusleṇku īpašība), tad jāpierāda, ka \(\sphericalangle A Y B=\sphericalangle M C B\).
Ar \(N\) apzīmēsim malas \(B C\) viduspunktu, bet ar \(T-\) taišņu \(AB\) un \(DN\) krustpunktu. Tā kā \(\sphericalangle B N T=\sphericalangle C N D\) (krustleņķi), \(BN=NC\) un \(\sphericalangle N B T=\sphericalangle N C D\) (iekšējie škērsleņķi pie paralēlām taisnēm \(AB\) un \(CD\) ), tad \(\triangle B N T=\triangle C N D\) pēc pazīmes \(\ell m \ell\). Tādā gadījumā to atbilstošās malas \(BT\) un \(CD\) ir vienādas, tātad
\[\frac{AB}{BT}=\frac{AB}{CD}\]
Ievērojam, ka \(\triangle BAX \sim \triangle DCX\) pēc pazīmes \(\ell \ell\), tātad\[\frac{AB}{CD}=\frac{AX}{CX}\]
Tā kā \(YX | CD\), tad no Talesa teorēmas iegūstam, ka\[\frac{A X}{X C}=\frac{A Y}{Y D}\]
No vienādībām iegūstam, ka\[\frac{A B}{B T}=\frac{A Y}{Y D}\]
Tātad \(\triangle YAB \sim \triangle DAT\) pēc pazīmes \(m \ell m\) un \(YB | DT\), tātad \(\sphericalangle AYB=\sphericalangle NDA\) kā kāpšļu leņķi. Tā kā \(\sphericalangle N D A=\sphericalangle M C B\) simetrijas dēļ vienādsānu trapecē, tad \(\sphericalangle AYB=\sphericalangle NDA=\sphericalangle MCB\). Tātad ap četrstūri \(BCMY\) var apvilkt riņķa līniju.