LV.VOL.2020.11.5 lv
Atrast lielāko naturālo skaitli \(N\), kuram ir spēkā īpašība: lai kuras \(N\) rūtiņas būtu aizkrāsotas \(4 \times 4\) rūtiņu tabulā, vienmēr varēs izvēlēties divas rindas un divas kolonnas tā, ka katra aizkrāsotā rūtiņa atrodas vai nu izvēlētajā rindā, vai izvēlētajā kolonnā (vai abās).
Atrisinājums
Lielākā \(N\) vērtība ir \(6\) . Pamatosim, ja iekrāsotas \(6\) rūtiņas, tad jebkuram krāsojumam izpildās uzdevuma nosacījumi. Ja kādā rindā ir vairāk nekā divas iekrāsotas rūtiņas, tad izvēlamies šo rindu un vēl kādu rindu, kurā ir kāda iekrāsota rūtiņa. Tātad izvēlētajās divās rindās jau ir vismaz četras iekrāsotas rūtiņas. Tā kā ir palikušas divas iekrāsotas rūtiņas, tad pietiek izvēlēties divas kolonnas, lai iekrāsotās rūtiņas atrastos šajās kolonnās.
Ja nevienā rindā nav vairāk kā divas iekrāsotas rūtiņas, tad pēc Dirihlē principa divas iekrāsotas rūtiņas ir vismaz divās rindās. Izvēlamies šīs divas (vai divas no trim, ja trīs rindās ir pa divām iekrāsotām rūtiņām) rindas. Tad izvēlētajās divās rindās jau ir tieši četras iekrāsotas rūtiņas. Tā kā ir palikušas divas iekrāsotas rūtiņas, tad pietiek izvēlēties divas kolonnas, lai iekrāsotās rūtiņas atrastos šajās kolonnās.
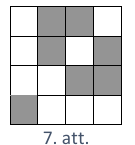
Pamatosim, ka lielākām \(N\) vērtībām īpašība nav spēkā visām tabulām. Ja \(N=7\), tad īpašība nav spēkā, piemēram, 7.att. dotajam rūtiņu izvietojumam. Ievērojam, ka, izvēloties jebkuras divas rindas, paliek trīs kolonnas, kurās atrodas iekrāsotās rūtiņas.