Atrisinājums

Dotos sešus iracionālos skaitļus attēlosim ar punktiem un savienosim divus punktus ar pelēku nogriezni, ja attiecīgo skaitļu summa ir racionāls skaitlis, un ar melnu, ja skaitļu summa ir iracionāls skaitlis.

Pierādīsim, ka eksistē tādi trīs punkti, kas visi savā starpā savienoti ar vienas un tās pašas krāsas nogriežņiem. Apskatām punktu \(A\). No tā iziet vismaz trīs nogriežņi, kas ir vienā un tajā pašā krāsā (izmantots Dirihlē princips). Nezaudējot vispārīgumu, varam pieņemt, ka nogriežņi \(AM, AN\) un \(AK\) ir pelēki (skat. 14.att.). Ja kaut viens no nogriežņiem \(MN, MK, NK\) ir pelēks, tad iegūstam pelēku trijstūri; ja tie visi ir melni, tad iegūstam melnu trijstūri \(MNK\).

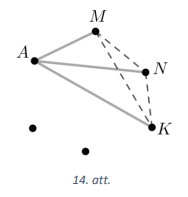
Pierādīsim, ka šis trijstūris, kam visas malas ir vienā krāsā, nav pelēks. Ja \(\alpha+\beta=c,\ \alpha+\gamma=b\) un \(\beta+\gamma=a\), kur \(a, b, c\) ir racionāli skaitļi, tad, saskaitot pirmās divas vienādības un ņemot vērā trešo vienādību, iegūstam, ka \(\alpha=\frac{c+b-a}{2}\) ir racionāls skaitlis (pretruna). Tātad vienkrāsainais trijstūris ir melns un tā virsotnēs ierakstītie skaitļi ir meklētie.