Atrisinājums

Sākotnējo rūtiņu laukumu šaha veidā izkrāsosim \(3 \times 3\) rūtiņas lielos melnos un baltos kvadrātos (skat. 14.att.).

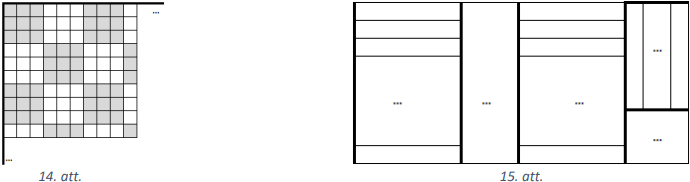
Katrs \(1 \times 6\) rūtiņu taisnstūris, neatkarīgi no novietojuma laukumā, satur tieši trīs melnas un trīs baltas rūtiņas. Tātad visi šādi taisnstūri kopā satur vienādu skaitu melno un balto rūtiņu.

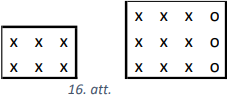
Pamatosim, ja ne \(n\), ne \(m\) nedalās ar \(6\), tad taisnstūrī \(n \times m\) melno un balto rūtiņu skaits nav vienāds, tas ir, šādu taisnstūri nevar sagriezt taisnstūros \(1 \times 6\) rūtiņas. Sadalām taisnstūri slejās, kuru platums ir \(6\) rūtiņas (skat. 15.att.), tajās melno un balto rūtiņu skaits ir vienāds. Labajā pusē noteikti atliek sleja, kuras platums ir mazāks nekā \(6\) rūtiņas. Šo sleju sadalām joslās, kuru augstums ir \(6\) rūtiņas, tajās melno un balto rūtiņu skaits ir vienāds. Labā apakšējā stūrī paliek taisnstūris, kura augstums ir mazāks nekā \(6\) rūtiņas. Līdz ar to nesadalīts paliek taisnstūris \(a \times b\), kura malu garumi var būt no \(1\) līdz \(5\) rūtiņām. Tā kā taisnstūris ir sagriezts taisnstūros \(1 \times 6\), tad \(a \cdot b\) dalās ar \(6\) un iespējami divi gadījumi \(2 \times 3\) vai \(4 \times 3\). Nevienā no šiem abiem taisnstūriem melno un balto rūtiņu skaits nav vienāds (skat. 16.att.). Tātad sākotnējā taisnstūrī melno un balto rūtiņu skaits nav vienāds un to nevar sadalīt taisnstūros \(1 \times 6\) rūtiņas.