LV.VOL.2010.10.5 lv
Vai kvadrātu ar izmēriem \(9 \times 9\) rūtiņas var sadalīt \(13\) taisnstūros ar izmēriem
\(2 \times 3\) rūtiņas un vienā stūrītī  ?
?
Atrisinājums
Pieņemsim, ka ir izdevies kvadrātu ar izmēriem \(9 \times 9\) rūtiņas sagriezt uzdevumā
prasītajās figūrās. Simetrijas dēļ var uzskatīt, ka šajā sadalījumā stūrītis ir
orientēts tieši tā kā redzams zīmējumā:  . (Ja tā nav, varam
kvadrātu pagriezt ap centru tā, lai stūrītis nonāk šādā stāvoklī.) Izkrāsosim kvadrātu
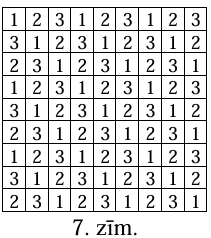
ar izmēriem \(9 \times 9\) rūtiņas trīs krāsās, kā parādīts 7.zīmējumā.
. (Ja tā nav, varam
kvadrātu pagriezt ap centru tā, lai stūrītis nonāk šādā stāvoklī.) Izkrāsosim kvadrātu
ar izmēriem \(9 \times 9\) rūtiņas trīs krāsās, kā parādīts 7.zīmējumā.
Katrā krāsā ir iekrāsots vienāds rūtiņu daudzums- pa \(27\) katrā krāsā. Katrs taisnstūris ar izmēriem \(2 \times 3\) rūtiņas pārklāj tieši divas katras krāsas rūtiņas, tātad \(13\) šādi taisnstūri kopā pārklāj pa \(26\) katras krāsas rūtiņām.
Tā kā stūrītis pārklāj divas vienas krāsas rūtiņas, tad prasītais sadalījums neeksistē.