Atrisinājums

Apzīmējam diagonālu krustpunktu ar \(O\); apzīmējam \(BD=d\) un \(OE=x\). Diagonāle \(B D\) ir kvadrāta simetrijas ass, tāpēc \(EA = EC\) (skat. 2. att.).

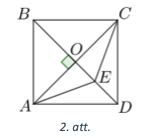
Kvadrāta diagonāles ir perpendikulāras un krustpunktā dalās uz pusēm, tāpēc trijstūris \(A O E\) ir taisnleṇķa trijstūris, kurā pēc Pitagora teorēmas iegūstam, ka \(E A^{2}=A O^{2}+O E^{2}=\left(\frac{d}{2}\right)^{2}+x^{2}\). Tādā gadījumā iegūstam:

\[\begin{gathered} E D \cdot E B+E A \cdot E C=(O D-O E)(O B+O E)+E A^{2}= \\ =\left(\frac{d}{2}-x\right)\left(\frac{d}{2}+x\right)+\left(\frac{d}{2}\right)^{2}+x^{2}=\left(\frac{d}{2}\right)^{2}-x^{2}+\left(\frac{d}{2}\right)^{2}+x^{2}=2 \cdot \frac{d^{2}}{4}=\frac{d^{2}}{2} . \end{gathered}\]

Izmantojot Pitagora teorēmu vienādsānu taisnleṇķa trijstūrī \(ABD\), iegūstam, ka \(A B^{2}+A D^{2}=B D^{2}\). Tā kā \(AB=AD\), tad \(2AB^{2}=d^{2}\) jeb \(AB^{2}=\frac{d^{2}}{2}\). Līdz ar to esam ieguvuši, ka \(ED \cdot EB+EA \cdot EC=\frac{d^{2}}{2}=AB^{2}\).