LV.NOL.2024.12.3 lv
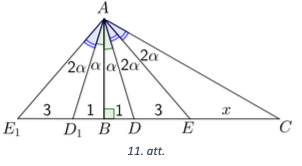
Taisnleṇķa trijstūrī \(ABC\left(\sphericalangle ABC=90^{\circ}\right)\) uz malas \(BC\) atlikti punkti \(D\) un \(E\) tā, ka \(\sphericalangle EAC=\sphericalangle DAE=2 \sphericalangle BAD\), \(BD=1, DE=3\). Aprēķināt \(EC\) garumu!
Atrisinājums
Apzīmēsim \(E C=x, \sphericalangle B A D=\alpha, \sphericalangle D A E=\sphericalangle E A C=2 \alpha\) un punktiem \(D\) un \(E\) atliksim attiecīgi simetriskus punktus \(D_{1}\) un \(E_{1}\) pret taisni \(A B\) (skat. 11. att.). Tātad \(B D_{1}=B D=1\) un \(D E=D_{1} E_{1}=3\). Izmantosim bisektrises īpašību vairākos trijstūros un nogriežṇu garumu vienādību \(A D_{1}=A D ; A E_{1}=A E\) (simetrijas dēl):
(1) \(\triangle D A C\) bisektrise \(A E: \quad \frac{A D}{A C}=\frac{D E}{E C}=\frac{3}{x}\);
(2) \(\triangle D_{1} A E\) bisektrise \(A D: \frac{A D_{1}}{A E}=\frac{D_{1} D}{D E} \Rightarrow \frac{A D}{A E}=\frac{2}{3}\);
(3) \(\triangle E_{1} AC\) bisektrise \(A D: \quad \frac{A E_{1}}{A C}=\frac{E_{1} D}{D C} \Rightarrow \frac{A E}{A C}=\frac{5}{3+x}\).
No (2) un (3) iegūstam, ka
\[\frac{A D}{A C}=\frac{A D}{A E} \cdot \frac{A E}{A C}=\frac{2}{3} \cdot \frac{5}{3+x}=\frac{10}{3(3+x)}.\]
Izmantojot **(1)**, iegūstam:\[\frac{10}{3(3+x)}=\frac{3}{x} \quad \Rightarrow \quad 10 x=27+9 x \quad \Rightarrow \quad x=27.\]
Tātad \(EC=x=27\).