Atrisinājums

Punkti \(P\) un \(Q\) jāatliek tā, ka \(A P=2 \mathrm{~cm}\) un \(A Q=5 \mathrm{~cm}\) (skat. 5. att.). Parādīsim, ka šādā gadījumā \(BP=7 \mathrm{~cm}\) un \(B Q=8 \mathrm{~cm}\).

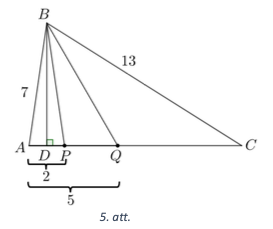
Pret malu \(AC\) novelkam augstumu \(BD\). Izmantojot Pitagora teorēmu trijstūros \(BDA\) un \(BDC\), iegūstam, ka \(AB^{2}-AD^{2}=BD^{2}=BC^{2}-DC^{2}\). Tā kā \(AC=12 \mathrm{~cm}\), tad varam izteikt, ka \(CD=12-AD\). Lîdz ar to iegūstam, ka

\[\begin{gathered} 7^{2}-A D^{2}=13^{2}-(12-A D)^{2} \\ 49-A D^{2}=169-\left(144-24 A D+A D^{2}\right) \\ 24 A D=24 \quad \Rightarrow \quad A D=1 \mathrm{~cm} \end{gathered}\]

Izmantojot Pitagora teorēmu trijstūrī \(ADB\), iegūstam, ka \(BD^{2}=AB^{2}-AD^{2}=48\). Tā kā \(D P=A P-A D=2-1=1 \mathrm{~cm}\), tad pēc Pitagora teorēmas \(\triangle BDP\) iegūstam, ka \(BP=\sqrt{BD^{2} + DP^{2}} = \sqrt{48+1}=7 \mathrm{~cm}\). Tā kā \(D Q=A Q-A D=5-1=4 \mathrm{~cm}\), tad pēc Pitagora teorēmas \(\triangle BDQ\) iegūstam, ka \(BQ = \sqrt{BD^{2}+DQ^{2}} = \sqrt{48+16} = 8 \mathrm{~cm}\). *Piezīmes* 1. Augstumu \(B D\) var aprēkināt arī, izmantojot trijstūra laukumu (pēc Hērona formulas). 2. Vajadzīgos punktus var iegūt, mēǵinot kombinēt dažādus malu garumus, lai iegūtu, ka hipotenūzas garums ir vesels skaitlis.