LV.NOL.2023.7.3 en lv
Dots četrstūris \(ABCD\), kuram visi leņķi ir mazāki nekā \(180^{\circ}\), \(\sphericalangle A=\sphericalangle B\), \(BC=1\) un \(AD=3\). Pierādīt, ka \(CD>2\).
Atrisinājums
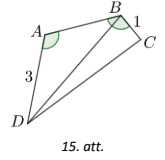
Novelkam nogriezni \(BD\) (skat. 15.att.). No dotā izriet, ka \(\sphericalangle DAB = \sphericalangle ABC > \sphericalangle ABD\). Tā kā trijstūrī \(ABD\) pret lielāku leņķi atrodas garāka mala, tad \(BD > AD=3\).
No trijstūra nevienādības trijstūrī \(BCD\) iegūstam, ka \(DC>DB-BC>3-1=2\).