Atrisinājums

Šahistus apzīmējam ar punktiem. Divus šahistus savienosim ar nepārtrauktu līniju, ja tie ir izspēēejuši partiju, bet ar pārtrauktu līiiju, ja tie nav izspēlējuši partiju.

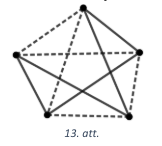
(A) Nē, var gadīties, ka nav tādu trīs šahistu, kas izspēlējuši vai nu 3, vai nevienu partiju, piemēram, skat. 13. att., kur nav neviena trijstūra, kuram visas malas ir viena veida līnijas.

(B) Pierādīsim, ka noteikti var atrast tādus trīs šahistus, kas kopā ir izspēlējuši vai nu 3 partijas, vai nevienu partiju, tas ir, ka var atrast tādu trijstūri, kuram visas malas ir viena veida līnijas.

Pieņemsim, ka nav neviena šāda trijstūra. Aplūkojam punktu \(A\). Tā kā no tā iziet \(5\) nogriežņi, tad vismaz trīs no tiem ir viena veida (pēc Dirihlē principa). Nezaudējot vispārīgumu, uzskatīsim, ka nogriežņi \(AB, AC, AD\) ir nepārtrauktas līnijas. Tad \(BC\) un \(CD\) jābūt pārtrauktām līnijām, bet tādā gadījumā trijstūrim \(ABD\) vai \(BCD\) visas malas būs viena veida līnijas (skat. 14. att.). Iegūta pretruna ar pieņēmumu.