LV.NOL.2018.9.5 lv
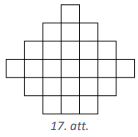
Dota figūra, kuras laukums ir \(24\) rūtiņas (skat. 17.att.). Griežot pa rūtiņu līnijām, tā sagriezta sešās vienlielās daļās (katras daļas laukums ir \(4\) rūtiņas). Noteikt, kāds ir mazākais iespējamais griezuma līniju kopgarums, pieņemot, ka rūtiņas malas garums ir viena vienība!
Atrisinājums
Dotās figūras perimetrs ir \(26\) vienības. Iegūto sešu daļu perimetrus apzīmējam ar \(p_{1}, p_{2}, p_{3}, p_{4}, p_{5}, p_{6}\) un aplūkojam summu \(p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6}\). Šajā summā katrs griezuma posms ir ieskaitīts divas reizes, bet katras daļas ārmalas posms - vienu reizi. Tad griezuma līniju kopgarumu var izteikt kā \(\frac{1}{2}\left(p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6}-26\right)\). Tātad nepieciešams minimizēt iegūto sešu daļu perimetru summu. Pavisam ir piecas dažādas figūras, kas sastāv no četrām rūtiņām (skat. 18.att.). Visām figūrām, izņemot \(2 \times 2\) kvadrātu, perimetrs ir \(10\) vienības, bet kvadrāta perimetrs ir \(8\) vienības. Pamatosim, ka no dotās figūras var izgriezt ne vairāk kā divus \(2 \times 2\) kvadrātus. Kvadrāts \(2 \times 2\) var atrasties tikai tajās vietās, kur kādā no kvadrāta rūtiņām atrodas "X" (skat. 19.att.). Ja kvadrātu novieto citās vietās, tad tas atšķeļ vienu atsevišķu rūtiņu. Tātad no dotās figūras var izgriezt ne vairāk kā divus \(2 \times 2\) kvadrātus. Līdz ar to mazākais iespējamais griezuma līniju kopgarums ir \((2 \cdot 8+4 \cdot 10-26):2=15\), to var iegūt, piemēram, kā parādīts 20.att.
