Atrisinājums

Mazākais skaits rūtiņu, kas jāiekrāso, ir \(7\). Tās var iekrāsot, piemēram, kā parādīts 17.att. Redzams, ka, izmetot jebkuras divas rindas, aizkrāsotas paliek vēl rūtiņas trīs dažādās kolonnās, tātad ar \(2\) kolonnu izmešanu visas atlikušās iekrāsotās rūtiņas izmest nevar.

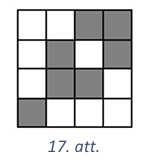
Pierādīsim, ka mazāk rūtiņu nevar iekrāsot, tas ir, ka sešas iekrāsotas rūtiņas vienmēr var izmest, izmetot divas rindas un divas kolonnas.

Ja kādā rindā ir \(3\) vai vairāk iekrāsotas rūtiņas, tad, izvēloties šo rindu, atliek vēl \(3\) vai mazāk rūtiņas, ko viegli izmest ar \(3\) gājieniem.

Ja nav tādas rindas, kurā ir \(3\) vai vairāk iekrāsotas rūtiņas, tad pēc Dirihlē principa noteikti ir rinda, kurā ir \(2\) iekrāsotas rūtiņas, izmetot to, paliek \(3\) rindas un \(4\) iekrāsotas rūtiņas, tātad atkal pēc Dirihlē principa ir vēl viena rinda, kurā ir \(2\) iekrāsotas rūtiņas. Izmetot arī to, atliek \(2\) iekrāsotas rūtiņas, kuras var izmest, izmetot divas kolonnas.