Atrisinājums

a) Lielākais skaits taisnstūru \(5 \times 13\), ko var izgriezt no rūtiņu lapas \(41 \times 65\), ir \(41\), piemēram, skat. 39.att. Vairāk taisnstūrus nav iespējams izgriezt, jo \((41 \cdot 65):(5 \cdot 13)=41\).

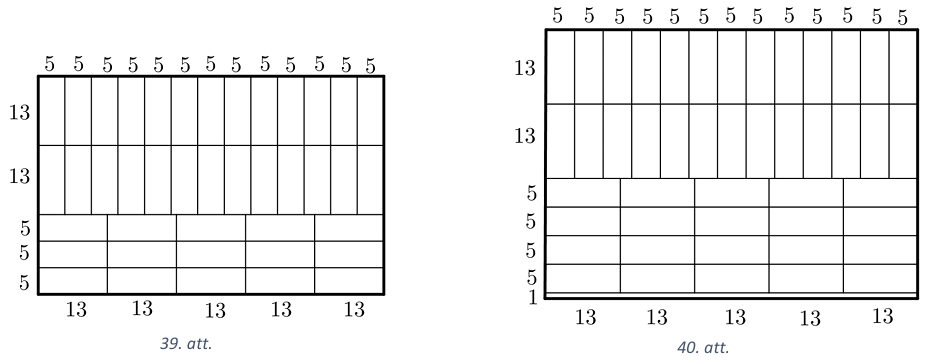
b) No rūtiņu lapas \(47 \times 65\) rūtiņas var izgriezt \(46\) taisnstūrus, skat., piemēram, 40.att.

Pierādīsim, ka \(47\) taisnstūrus izgriezt nevar. Ja varētu izgriezt \(47\) taisnstūrus, tad visa sākotnējā rūtiņu lapa būtu jāsagriež \(5 \times 13\) rūtiņu taisnstūros. Pieņemsim, ka tas ir izdevies un aplūkosim \(47\) rūtiņu garo malu. Pieņemsim, ka pie šīs malas pieskaras \(m\) taisnstūri ar garo malu (13) un \(n\)- ar īso malu (5), tad \(13m+5n=47\). Pamatosim, ka šim vienādojumam nav atrisinājuma nenegatīvos veselos skaitļos. Ja \(m \geq 4\), tad vienādojuma kreisās puses izteiksmes vērtība ir vismaz \(13 \cdot 4+5n \geq 52 > 47\), tātad \(m < 4\). Pārbaudām visas iespējamās \(m\) vērtības:

• ja \(m=0\), tad \(n=\frac{47}{5}\)
• ja \(m=1\), tad \(n=\frac{34}{5}\)
• ja \(m=2\), tad \(n=\frac{21}{5}\)
• ja \(m=3\), tad \(n=\frac{8}{5}\)

Nevienā gadījumā \(n\) nav nenegatīvs vesels skaitlis. Tātad \(47\) taisnstūros doto lapu sagriezt nav iespējams.