Atrisinājums

Mazākais iespējamais griezuma līniju kopgarums ir \(24\) vienības, skat., piemēram, 30.att.

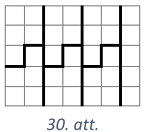
Pierādīsim, ka nav iespējams iegūt mazāku griezuma līniju kopgarumu. Pieņemsim, ka taisnstūris ir sagriezts \(7\) daļās, kuru perimetri ir \(P_{1}, P_{2}, \ldots, P_{7}\), un griezuma līniju kopgarums ir \(L\). Aplūkojam summu \(P_{1}+P_{2}+\ldots+P_{7}\). Šajā summā katrs griezuma posms ir ieskaitīts divas reizes, bet katras daļas ārmalas posms - vienu reizi. Tā kā taisnstūra perimetrs ir \((7+5) \cdot 2=24\), tad iegūstam \(P_{1}+P_{2}+\ldots+P_{7}=2 L+24\) jeb \(L=\frac{P_{1}+P_{2}+\ldots+P_{7}-24}{2}\). Tātad \(L\) būs minimāls, ja perimetru summa būs vismazākā. Apskatīsim, kādas figūras, kuru laukums ir \(5\) rūtiņas, var iegūt, griežot pa rūtiņu līnijām. Figūru, ko iegūst no pieciem vienības kvadrātiem, pievienojot tos vienu otram pa vesela garuma malām, sauc par pentamino. Pavisam ir \(12\) dažādi pentamino (skat. 31.att.).

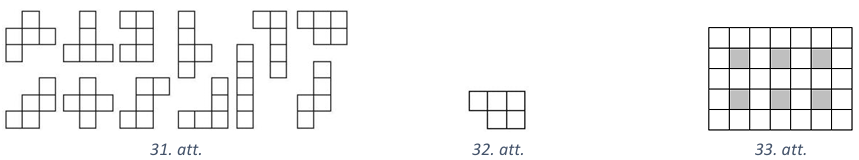
No visām pentamino figūrām mazākais perimetrs ir 32.att. dotajai figūrai un tas ir \(10\) vienības, pārējām figūrām perimetrs ir \(12\).

Tagad pierādīsim, ka doto taisnstūri nevar sagriezt \(7\) šādās figūrās. lekrāsojam rūtiņas, kā redzams 33.att., ievērojam, ka katra 32.att. figūriņa aizņem vismaz vienu iekrāsoto rūtiņu. Tad, ja būtu izdevies sagriezt taisnstūri \(7\) šādās figūrās, tad būtu vajadzīgas vismaz \(7\) iekrāsotās rūtiņas, bet ir tikai \(6\), pretruna.

Tātad ir ne vairāk kā sešas 32.att. figūras un septītā figūra ir citādāka, turklāt tās perimetrs ir \(12\). Līdz ar to perimetru summa ir vismaz \(6 \cdot 10+12=72\), un griezuma līniju garumu summa \(L \geq \frac{72-24}{2}=24\).