LV.NOL.2011.8.4 lv
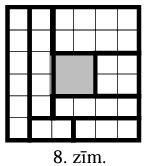
Apskatām zīmējumā parādīto figūru, kas sastāv no \(32\) rūtiņām. Kāds ir lielākais dažādu
taisnstūru skaits, kuros to var sagriezt (griezumus jāveic tikai pa rūtiņu malām)?
Atbildi pamato! (Divus taisnstūrus uzskata par atšķirīgiem, ja tiem atšķiras izmēri
nevis tikai novietojums, piemēram, 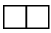 un
un  ir vienādi taisnstūri.)
ir vienādi taisnstūri.)

Atrisinājums
Figūru var sagriezt augstākais \(7\) dažādos taisnstūros, piem., skat. 8.zīm.
Ja to sagrieztu tādos taisnstūros, kuru laukums nepārsniedz \(6\) rūtiņas, tad to laukumu summa nepārsniegtu \(1+2+3+4+4+5+6+6=31 < 32\) (šie taisnstūri ir ar izmēriem \(1 \times 1,1 \times 2\), \(1 \times 3,1 \times 4,2 \times 2,1 \times 5,1 \times 6\) un \(2 \times 3\) rūtiņas).
Tāpēc, figūru sagriežot kaut kādā skaitā taisnstūru, kāda iegūtā taisnstūra laukums būs vismaz \(8\). Pie tam, neviena taisnstūra laukums nebūs vienāds ar \(7\). Tāpēc, ja figūru sagrieztu vismaz \(8\) dažādos taisnstūros, tad to laukumu summa, ievērojot visu augstākminēto, būtu vismaz \(1+2+3+4+4+5+6+8=33 > 32\)- pretruna. Tāpēc \(7\) ir lielākais dažādo taisnstūru skaits, kuros figūru var sagriezt.