LV.NOL.2008.11.2 lv
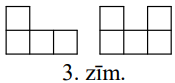
Kvadrāts sastāv no \(n \times n\) vienādām kvadrātiskām rūtiņām. Ir zināms, ka to var sagriezt tādos gabalos, kādi parādīti 3.zīm., pie tam viena veida gabalu ir tikpat, cik otra. Atrast mazāko iespējamo \(n\) vērtību.
Atrisinājums
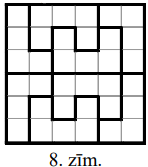
Apzīmēsim katra veida figūru skaitu ar \(k\); tad tās kopā satur \(4k+5k=9k\) rūtiņas. Iegūstam vienādību \(9k=n^{2}\), tātad \(n\) dalās ar \(3\). Mazākās iespējamās \(n\) vērtības ir \(n=3\) un \(n=6\). Vērtība \(n=3\) acīmredzami neder. Atrisinājumu pie \(n=6\) skat. 8.zīm.