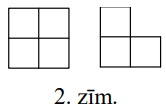
Atrisinājums

Ja katra veida figūru ir \(k\), tad kopējais rūtiņu skaits tajās ir \(4k+3k=7k\); tātad \(n^{2}=7k\) un \(n\) jādalās ar \(7\). Mazākās iespējamās \(n\) vērtības ir \(n=7\) un \(n=14\).

A. Pie \(n=7\) uzdevuma prasības nav izpildāmas. Pieņemsim, ka tas izdevies, un izkrāsosim rūtiņas, kā parādīts 5.zīm. Katrs no \(7\) kvadrātiem satur \(2\) melnas rūtiņas, tāpēc \(7\) "stūrīši" kopā satur \(28-14=14\) melnas rūtiņas. Tāpēc katrs "stūrītis" satur tieši \(2\) melnas un \(1\) baltu rūtiņu (jo katrs stūrītis noteikti satur ne vairāk kā \(2\) melnas rūtiņas). Bet melnās rūtiņas nevar sadalīties pa pāriem, kas ietilpst kvadrātos un stūrīšos, jo katrā rindiņā, kurā tās vispār ir, tās ir nepāra skaitā.

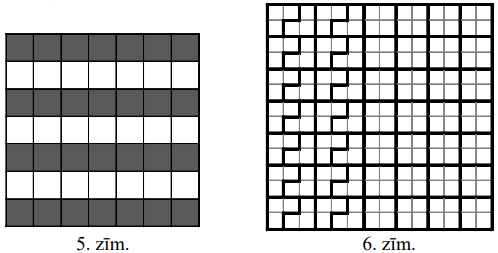
B. Risinājumu pie \(n=14\) skat. 6.zīm.