LV.NOL.2004.12.5 lv
Parlamentā ir \(100\) deputātu. Ir zināms, ka nevienam deputātam nav aizspriedumu pret vairāk nekā \(2\) citiem deputātiem. (Ja \(A\) ir aizspriedumi pret \(B\), tad \(B\) var arī nebūt aizspriedumu pret \(A\).)
Kāds ir mazākais komisiju skaits, kurās noteikti var sadalīt jebkura šāda parlamenta deputātus (katram deputātam jāpiedalās vismaz vienā komisijā) tā, ka nevienā komisijā nevienam deputātam nav aizspriedumu ne pret vienu citu?
Atrisinājums
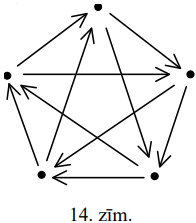
(A) Var gadīties, ka ir \(5\) deputāti, kuru "aizspriedumu struktūra" attēlota 14.zīm. Nekādus divus no tiem nevar iekļaut vienā komisijā. Tātad var gadīties, ka nepieciešamas vismaz \(5\) komisijas.
(B) Parādīsim, ka ar \(5\) komisijām vienmēr pietiek. Pierādīsim to ar matemātisko indukciju patvaļīgam deputātu skaitam \(n\). Pie \(n=1;\ 2;\ 3;\ 4;\ 5\) tas ir acīmredzams (katrā komisijā iekļauj vienu deputātu).
Pieņemsim, ka apgalvojums ir pareizs pie \(n=1;\ 2;\ 3;\ \ldots\); \(m-1\), kur \(m \geq 6\). Apskatīsim \(m\) deputātus. Ja katru no šiem deputātiem "ienīst" vairāk nekā \(2\) citi, tad kopējais "ienaidu" skaits ir lielāks par \(2m\), tā ir pretruna, jo katram deputātam ir aizspriedumi pret augstākais \(2\) citiem, tāpēc "ienaidu" nav vairāk par \(2m\).
Tāpēc eksistē deputāts \(A\), pret kuru aizspriedumu nav vairāk kā \(2\) citiem. Apskatīsim visus \(m-1\) deputāus, izņemot \(A\). Saskaņa ar induktīvo hipotēzi tos var sadalīt \(5\) komisijās vajadzīgā veidā. Deputāts \(A\) ir "nepieņemams" ne vairāk kā \(4\) no tām (jo ir \(\leq 2\) deputāti, kam ir aizspriedumi pret viņu, un ir \(\leq 2\) deputāti, pret kuriem viņam ir aizspriedumi). Tātad \(A\) var pievienot vismaz \(1\) komisijai. Induktīvā pāreja izdarīta.