LV.AMO.2024.9.5 lv
Ingai ir tālrunis ar šādu pogu izkārtojumu:
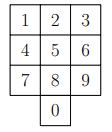
Viṇas draudzenes Zanes deviņciparu tālruņa numuram ir šādas īpašības:
- visi Zanes tālruņa numura cipari ir atšk̦irīgi;
- pirmie četri cipari ir sakārtoti augošā secībā un to attiecīgo pogu centri veido kvadrātu;
- pēdējo četru ciparu pogu centri arı̄ veido kvadrātu;
- Zanes tālruņa numurs dalās ar \(15\).
Cik ir tādu deviņciparu tālruņa numuru, kas varētu būt Zanes tālruņa numurs?
Atrisinājums
Pamatosim, ka atbilde ir 12 dažādi skaitļi. Vispirms uzrakstīsim visas pogas, kuru centri veido kvadrātu:
\[\begin{gathered} (1,2,4,5);\;\;\;\; (1,3,7,9);\\ (4,5,7,8);\;\;\;\; (2,4,6,8);\\ (2,3,5,6);\;\;\;\; (0,5,7,9);\\ (5,6,7,8). \end{gathered}\]
Taču ievērojam, ka mēs nevaram izmantot nevienu no kvadrātiem, kas atrodas kreisajā kolonnā, jo tad tā cipari atkārtotos ar kādu no cita kvadrāta. Tā kā numuram jādalās ar \(15\), tad pēdējie četri cipari noteikti būs \(0,5,7,9\), jo skaitlim jādalās ar \(5\). To secību noskaidrosim vēlāk. Tā kā mēs jau esam izmantojuši skaitlus \(7\) un \(9\), tad pirmajiem četriem cipariem jābūt \(2,4,6,8\) tieši šādā secībā, jo tie ir sakārtoti augoši. Vienīgie atlikušie cipari, kas varētu atrasties tālruņa numura vidū, ir \(1\) un \(3\). Tā kā numuram ir jādalās ar 3 (tas dalās ar 15), tad visu ciparu summai ir jādalās ar 3 . Iegūstam, ka \(2+4+6+8+x+0+5+7+9=41+x\) jādalās ar \(3\), kur \(x\) ir \(1\) vai \(3\). Tātad vienīgā iespēja ir tad, ja \(x=1\). Esam ieguvuši, ka Zanes numurs ir izskatā\[24681 \ast \ast \ast \ast,\]
kur pēdējie 4 cipari ir kāds no skaitļiem \(0,5,7,9\). Tā kā numuram ir jādalās ar \(5\), tad pēdējais cipars var būt \(0\) vai \(5\). Tātad pēdējam ciparam ir divas opcijas. Pirmspēdējam ciparam nav šādu ierobežojumu, tāpēc tas var būt jebkurš no atlikušajiem \(3\) cipariem, tāpēc tam ir trīs opcijas. Simtu pozīcijā arı̄ varam ielikt jebkuru no atlikušajiem cipariem, tāpēc iegūstam divas opcijas. Atlikušo skaitli tad liekam tūkstošu pozīcijā. Kopumā mums ir \(2 \cdot 3 \cdot 2 \cdot 1=12\) dažādi veidi, kā iegūt tālruņa numuru, kam izpildās īpašības, kas piemīt Zanes tālruṇa numuram.