LV.AMO.2024.9.4 lv
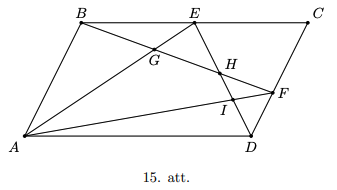
Uz paralelograma \(ABCD\) malām \(BC\) un \(CD\) atzīmēti attiecīgi punkti \(E\) un \(F\). Nogriežņu \(AE\) un \(BF\) krustpunkts ir \(G\), nogriežņu \(AF\) un \(ED\) krustpunkts ir \(I\), bet \(BF\) un \(ED\) krustpunkts ir \(H\). Pamatot, ka \(S_{AGHI} = S_{BEG}+S_{CEHF}+S_{DFI}\).
Atrisinājums
Ievērosim, ka \(S_{AED}=\frac{1}{2} S_{ABCD}\), jo trijstūra \(AED\) mala \(A D\) sakrīt ar paralelograma malu un arī to attiecīgie augstumi sakrīt. Līdzīgi spriežot, varam secināt, ka \(S_{FBC}+S_{DAF}=\frac{1}{2} S_{ABCD}\), jo abu šo trijstūru pamatu summa, tas ir, \(DF+FC\) sakrīt ar paralelograma malu \(DC\) un augstumi trijstūrī pret šīm malām sakrīt ar paralelograma augstumu. Tātad iegūstam, ka \(S_{AED}=S_{FBC}+S_{DAF}\), bet \(S_{AED}=S_{AGHI}+S_{GEH}+S_{AID}\), \(S_{FBC}=S_{BEG}+S_{GEH}+S_{CEHF}\) un \(S_{DAF}=S_{AID}+S_{DFI}\) (skatīt 15. att.). Apvienojot šīs izteiksmes, iegūstam, ka
\[\begin{gathered} S_{AGHI}+S_{GEH}+S_{AID} = S_{BEG}+S_{GEH}+S_{CEHF}+S_{AID}+S_{DFI},\\ S_{AGHI} = S_{BEG}+S_{CEHF}+S_{DFI}, \end{gathered}\]
kas arı̄ ir prasītā vienādība.